Atelier D2E
Utilisation de modèles de régression à coefficients variant dans le temps dans le cadre de la prévision conjoncturelle
16 mars 2023
Introduction
Sur longue période, les institutions, les normes de sociétés ainsi que les comportements des agents économiques évoluent, induisant des changements dans la dynamique des séries économiques étudiées.
De nombreux modèles de l’Insee sont basés sur des régressions linéaires (CJO, prévisions, calage…) qui supposent que les relations entre les variables sont fixes dans le temps.
Hypothèse vraie sur le court-terme mais généralement fausse sur le long-terme ou en présence de changements structurels (changement de nomenclature, de définition, COVID…)
Objectifs :
étudier des méthodes qui permettent de relâcher cette contrainte ;
proposer une façon simple d’implémenter et de comparer ces méthodes (package
tvCoef)
Modèle de régression linéaire
Idée générale :
\[ \DeclareMathOperator{\argmin}{argmin} y_t=\beta_0+\beta_1 x_{1,t}+\dots+\beta_p x_{p,t} +\varepsilon_t \]
\[ y_t=\beta X_t+\varepsilon_t \]
Estimé grâce à la méthode des moindres carrés ordinaires
Exemple simple : prévision du PIB à partir du climat des affaires France (au mois 2) en niveau et en différence
\[ PIB_t = \beta_0 + \beta_1 climat\_fr_t + \beta_2 \Delta climat\_fr_t + \varepsilon_t \]
Estimation entre 2000 T1 et 2019 T4 :
\[ PIB_t = -2,09 + 0,02 \times climat\_fr_t + 0,04 \times \Delta climat\_fr_t + \varepsilon_t \]
Deux types d’estimations : estimations dans l’échantillon et estimations en temps réel.
- Dans l’échantillon : utilise toutes les données disponibles pour estimer les valeurs au sein de l’échantillon. Ce sont les valeurs ajustées qu’on obtient après une régression linéaire.
- En temps réel : prévisions hors échantillon qui prévoient des valeurs en dehors d’un échantillon de données.
Modèle estimé jusqu’à \(t\) pour effectuer la prévision de \(t+1\), puis on recommence en estimant le modèle jusqu’à \(t+1\).
Qualité des modèles évaluée par l’analyse des résidus et le calcul du RMSE (root mean square error) :
\[ \sqrt{\frac{\sum_{t=1}^{T} (PIB_t - \widehat{PIB}_t)^2}{T}} \]
Objectifs
Comparer différentes méthodes pour modéliser et estimer :
\[ PIB_t = \beta_{0,t} + \beta_{1,t} climat\_fr_t + \beta_{2,t} \Delta climat\_fr_t + \varepsilon_t \]
Idée : rester proche du cas de la régression linéaire pour que les résultats restent facilement interprétables.
Plan :
- Les tests statistiques étudiés
- Les régressions par morceaux
- Les régressions locales
- Les modèles espace-état
- Quelques résultats généraux
Tests statistiques : Bai et Perron
On cherche à savoir si les coefficients sont stables au cours du temps.
Bai et Perron s’appuie sur le test de Chow. Proposent un algorithme efficace pour trouver les dates de ruptures (package strucchange). Soit le modèle :
\[ PIB_t = \beta_0 + \beta_1 climat\_fr_t + \beta_2 \Delta climat\_fr_t + \varepsilon_t \]
On le sépare en deux, autour d’une date \(t_1\), et on obtient deux sous-modèles :
\[ \forall t \leq t_1 :\quad PIB_t = \beta_0' + \beta_1' climat\_fr_t + \beta_2' \Delta climat\_fr_t + \varepsilon_t \]
\[ \forall t > t_1 :\quad PIB_t = \beta_0'' + \beta_1'' climat\_fr_t + \beta_2'' \Delta climat\_fr_t + \varepsilon_t \]
L’hypothèse nulle suppose que \(\beta_0' = \beta_0''\), \(\beta_1' = \beta_1''\) et \(\beta_2' = \beta_2''\). Autrement dit, on teste si les deux modèles obtenus sont significativement différents.
Limites de Bai Perron
- La rupture peut n’être que sur un sous-ensemble de variables, mais le test ne s’applique que sur l’ensemble d’un modèle
On teste :
\[ PIB_t = (\beta_{0} + \beta_{1} climat\_fr_t + \beta_{2} \Delta climat\_fr_t) \mathbb 1_{t \leq t_1} + \\ (\beta_{0}' + \beta_{1}' climat\_fr_t + \beta_{2}' \Delta climat\_fr_t)\mathbb 1_{t > t_1} + \varepsilon_t \]
On ne peut pas tester :
\[ PIB_t = \beta_{0} + \beta_{1} climat\_fr_t + (\beta_{2} \mathbb 1_{t \leq t_1}+ \beta_{2}' \mathbb 1_{t > t_1})\Delta climat\_fr_t + \varepsilon_t \]
- Instabilité sur le choix de la date et la rupture n’est pas forcément brutale (ex : évolution lente dans le temps)
Mais ces tests supposent qu’il existe une date de rupture à déterminer, alors que l’on veut parfois juste savoir si les coefficients sont constants ou non.
Nyblom et Hansen
Tests trouvés dans la littérature autour de Nyblom et Hansen (1992) : sous tvCoef::hansen.test() \[
\begin{cases}
(H_0):&\text{coefficients constants} \\
(H_1):&\text{coefficients suivent une martingale}
\end{cases}
\]
Limites de Hansen :
Test de la l’instabilité de la variance (passer par d’autres tests)
Test joint ne s’applique pas aux indicatrices
Ne s’applique que sur les variables stationnaires
Comme tout test, ils ont leurs limites, prendre les résultats avec précaution.
Ex : même si le test de Hansen ne détecte pas d’instabilité, le test de Bai et Perron peut néanmoins détecter des ruptures.
Régressions linéaires par morceaux
Modèles les plus simples :
\[ \exists t_1,\dots,t_{T-1}:\: \beta_t = \beta_1\mathbb 1_{t \leq t_1} + \beta_2 \mathbb 1_{t_1 < t \leq t_2} + \dots + \beta_T \mathbb 1_{t_{T-1} < t} \]
S’estiment en :
Découpant les régresseurs (\(\mathbb V[\varepsilon_t]\) fixe dans le temps)
tvCoef::piece_reg()Ou en faisant des régressions linéaires par morceaux (\(\mathbb V[\varepsilon_t]\) varie par sous-période)
tvCoef::bp.lms()
utilisation du cas 1 car donne une seule régression en sortie.
Dans les deux cas estimations de coefficients restent les mêmes. Différences : sur les variances et sur les estimations en temps réel.
Avantages :
Simples à comprendre et à implémenter
Facilement combinable avec d’autres types de modèles (régressions locales)
Inconvénients :
Suppose l’existence une rupture brutale
Imprécisions dans le choix de la date
Dans le cas de notre modèle exemple, Bai et Perron détecte une rupture en 2011 T1. Le modèle suivant est donc estimé :
\[ PIB_t = (\beta_{0,t}+ \beta_{1,t}climat\_fr_t + \beta_{2,t} \Delta climat\_fr_t) \mathbb{1} _{t \leq 2011} + \\ (\beta_{0,t} + \beta_{1,t} climat\_fr_t + \beta_{2,t} \Delta climat\_fr_t) 1_{t > 2011} + \varepsilon_t \]
Ce qui donne :
\[ PIB_t = (-2,9+ 0,03 \times climat\_fr_t + 0,07 \times \Delta climat\_fr_t) \mathbb{1} _{t \leq 2011} + \\ (-1,04 + 0,01 \times climat\_fr_t - 0,01 \times \Delta climat\_fr_t) 1_{t > 2011} + \varepsilon_t \]
Régressions locales : tvreg
Hypothèse \(\beta_t = \beta(z_t)\) avec par défaut \(z_t = t/T\) et \(\beta()\) localement constante (Nadaraya-Watson) ou localement linéaire.
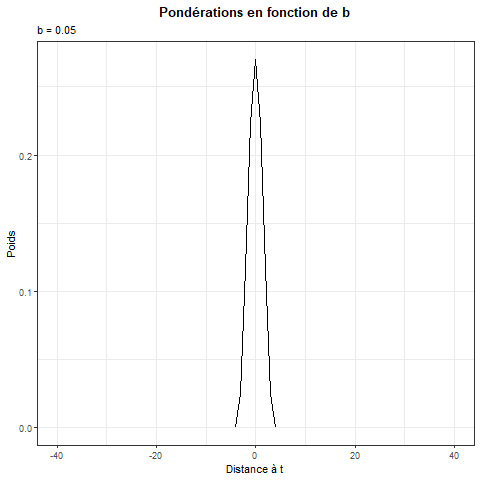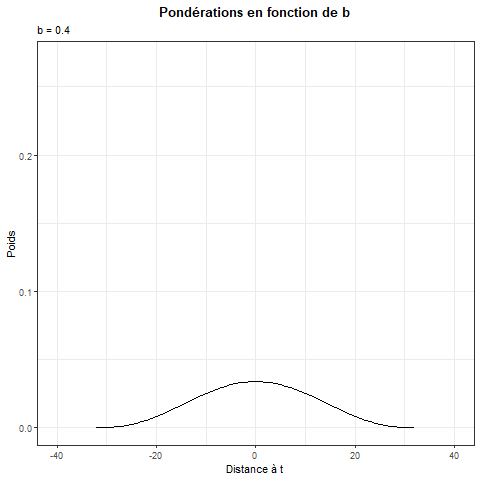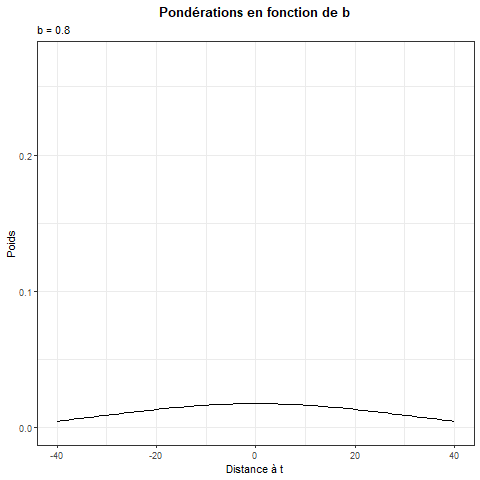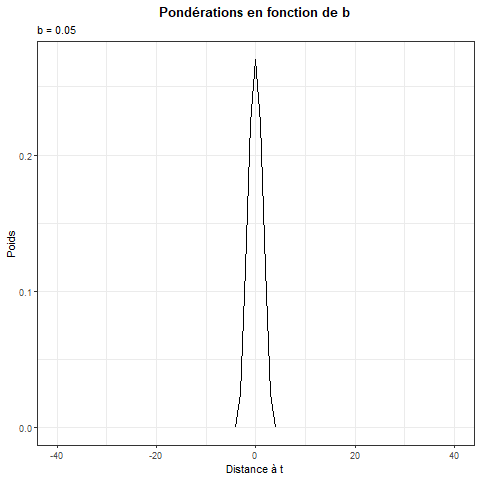
Estimation : \[ \beta(z_t) = \underset{\theta_0}{\argmin}\sum_{j=1}^T\left(y_{j}-x_j\theta_0\right)^2K_b(z_j-z_t) \] Avec \(K_b(x)=\frac 1 b K(x/b)\) une fonction de noyau pour pondérer les observations.
Remarque :
- Si \(b\geq1\) on utilise toutes les données pour chaque estimation.
- Si \(b \rightarrow 20\) le poids associé à chaque donnée tend à devenir le même pour toutes, estimation \(\simeq\) à la régression linéaire
Inconvénient :
- Tous les coefficients varient
- Problème du choix de \(b\) : par validation croisée (entre 0 et 20) mais peu discriminant
- Fortes révisions possibles en temps-réel : ajout d’un point, changement de b, noyau asymétrique
Remarque :
Possibilité de combiner les précédents modèles en estimant une régression locale sur des données coupées
En effectuer deux régression, on peut fixer les coefficients de certaines variables.
Modèles espace-état
Modélisation espace-état est une méthodologie générale qui permet de traiter un grand nombre de problèmes de séries temporelle.
Hypothèse : problème déterminé par une série de vecteurs non observés \(\alpha_1,\dots,\alpha_n\) associés aux observations \(y_1,\dots,y_n\), la relation entre \(\alpha_t\) et \(y_t\) étant spécifiée par le modèle espace-état.
Plusieurs formes de modèles sont possibles, les plus simples étant les modèles linéaires gaussiens.
Version simplifiée :
\[ \begin{cases} y_t=X_t\alpha_t+\varepsilon_t,\quad&\varepsilon_t\sim\mathcal N(0,\sigma^2)\\ \alpha_{t+1}=\alpha_t+\eta_t,\quad&\eta_t\sim\mathcal N(0,\sigma^2 Q) \end{cases},\text{ avec }\eta_t\text{ et }\varepsilon_t\text{ indépendants} \]
avec \(y_t\) de dimension \(p\times 1\) vecteur des observations, et \(\alpha_t\) de dimension \(m \times 1\) vecteur d’états (state vector).
\(\sigma^2\) un facteur simplifiant les estimations (Concentration of loglikelihood).
Retour sur la régression linéaire
Régression linéaire : \[ \begin{cases} y_t=X_t\alpha+\varepsilon_t,\quad&\varepsilon_t\sim\mathcal N(0,\sigma^2)\\ \alpha_{t+1}=\alpha_t=\dots=\alpha_0=\alpha \end{cases} \] C’est-à-dire : \[ PIB_t = \beta_0 + \beta_1 climat\_fr_t + \beta_2 \Delta climat\_fr_t + \varepsilon_t \] Devient : \[ PIB_t=\begin{pmatrix}1 & climat\_fr & \Delta climat\_fr\end{pmatrix}_t \begin{pmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{pmatrix} + \varepsilon_t \]
Estimation par filtre de Kalman
Deux opérations classiques : filtering et smoothing
- Smoothing : estime le coefficient à chaque date grâce à toute l’information disponible. Ce qui est proche des estimations dans l’échantillon.
\[ \hat\alpha_t = E[\alpha_t|y_0, \dots, y_n] \] Ex : régression linéaire : \(\hat\alpha_t = \hat \alpha\)
- Filtering : estime le coefficient suivant (en \(t+1\)) avec les informations connues en \(t\). Ce qui est proche des estimations en temps-réel.
\[ a_{t+1} = E[\alpha_{t+1}|y_0, \dots, y_t] \]
Ex : régression linéaire : \(a_{2010T2} = \hat \alpha\) estimé en utilisant les données jusqu’en 2010T1
Résultats
Etude de 25 modèles de prévision de la production manufacturière estimés entre 1990 T1 et 2019 T4. On estime les différents modèles présentés dans l’échantillon et en temps réel, puis on compare les RMSE des modèles par rapport au modèle linéaire. Enfin on fait des moyennes par secteur.
On obtient les résultats suivants pour les estimations dans l’échantillon :
| Reg linéaire | Espace état | Reg morceaux | Reg locale + morceaux | Reg locale | |
|---|---|---|---|---|---|
| model_c1 (7) | 1 | 0,97 | 1,00 | 1,00 | 1,00 |
| model_c3 (5) | 1 | 0,85 | 0,93 | 0,90 | 0,94 |
| model_c4 (5) | 1 | 0,81 | 0,96 | 0,90 | 0,90 |
| model_c5 (5) | 1 | 0,75 | 0,80 | 0,78 | 0,78 |
| model_manuf (3) | 1 | 0,96 | 0,99 | 0,97 | 0,98 |
La plupart des modèles sont généralement meilleurs que le modèle linéaire.
Et en temps réel :
| Reg linéaire | Espace état | Reg morceaux | Reg locale + morceaux | Reg locale | |
|---|---|---|---|---|---|
| model_c1 (7) | 1 | 0,99 | 1,00 | 1,00 | 1,00 |
| model_c3 (5) | 1 | 0,91 | 2,73 | 2,74 | 0,99 |
| model_c4 (5) | 1 | 0,92 | 5,13 | 5,19 | 1,06 |
| model_c5 (5) | 1 | 0,87 | 2,58 | 2,75 | 1,26 |
| model_manuf (3) | 1 | 0,96 | 1,01 | 1,03 | 1,00 |
Les modèles espace-état sont meilleurs que le modèle linéaire en terme de RMSE pour la prévision en temps réel. Pour ce qui est des autres modèles, plus variable d’un modèle à l’autre.
Conclusion
- De nombreux modèles peuvent être estimés autour des régressions linéaires : le cadre reste simple mais la modélisation est plus complexe
choix de modélisations doivent être faits
- Même s’ils peuvent améliorer les performances des modèles « classiques » ils ne les remplacent pas pour autant
- Modèles parfois complexes à implémenter (notamment espace-état)
tvCoefpeut vous aider (https://github.com/AQLT/tvCoef)
À venir
Court-terme : pause de 10/15 minutes suivie d’un atelier pratique :
https://aqlt.github.io/AteliertvCoef/
Sur tvCoef : documentation, gestion des retards de la variable endogène, amélioration des estimations en temps réel autour de la date de rupture des régressions par morceaux
Autour cette l’étude : séminaire D2E + document de travail
Autres études : analyse de ces méthodes pour la CJO