1 - R et JDemetra+

Désaisonnaliser une série temporelle

Auteur

Alain Quartier-la-Tente

L’objectif de ce TP est d’apprendre à manipuler JDemetra+ sous R à travers le package RJDemetra V3.

Pour manipuler JDemetra+ sous R il y a actuellement deux façons :

Utiliser le JWSACruncher qui permet, à partir de la console, de mettre à jour un workspace JDemetra+ et d’exporter les résultats sans devoir ouvrir le logiciel. Pour faciliter son utilisation depuis R, le package rjwsacruncher peut être utilisé (voir TP5 - JDemetra+ en production).
Utiliser les packages R associés à JDemetra+ qui permettent d’effectuer des désaisonnalisations avec les mêmes algorithmes et paramètres que JDemetra+ et de manipuler des workspaces.

Dans ce TP on utilisera les données du package RJDemetra mais n’hésitez pas à utiliser vos propres séries !

Pour faire de la désaisonnalisation sous R il existe plusieurs packages :

seasonal et x12 qui permettent de faire du X-13ARIMA-SEATS en utilisant les programmes du US Census Bureau
RJDemetra qui est une interface R à JDemetra+ 2.x.y.
Un ensemble de packages associés à JDemetra+ 3.x.y disponibles à l’addresse https://github.com/rjdverse. C’est ce que l’on utilisera dans ce TP. Ces packages nécessite d’avoir avoir Java 17 ou plus. En cas de problème d’installation voir le manuel d’installation .

Dans cette formation, nous utiliserons les packages suivants RJDemetra, rjd3toolkit, rjd3tramoseats, rjd3providers, rjd3workspace :

packages_to_install <- c("RJDemetra", "rjd3toolkit", "rjd3x13", "rjd3tramoseats", "rjd3providers", "rjd3workspace")

packages <- packages_to_install[! packages_to_install %in% installed.packages()[,"Package"]]
if (length(packages) > 0) {
  install.packages(
    packages, 
    repos = c("https://aqlt.r-universe.dev", "https://cloud.r-project.org")
  )
}

1 Créer une specification

Les modèles autour de la méthode X-13ARIMA peuvent être estimés avec rjd3x13::x13(), rjd3x13::regarima()) et rjd3x13::x11().

Les spécifications peuvent être crées avec les fonctions rjd3x13::spec_regarima, rjd3x13::spec_x11() ou rjd3x13::spec_x13() et peuvent être modifiées par :

Pour le préajustement : rjd3toolkit::set_arima(), rjd3toolkit::set_automodel(), rjd3toolkit::set_basic(), rjd3toolkit::set_easter(), rjd3toolkit::set_estimate(), rjd3toolkit::set_outlier(), rjd3toolkit::set_tradingdays(), rjd3toolkit::set_transform(), rjd3toolkit::add_outlier(), rjd3toolkit::remove_outlier(), rjd3toolkit::add_ramp(), rjd3toolkit::remove_ramp(), rjd3toolkit::add_usrdefvar() ;
Pour la décomposition : rjd3x13::set_x11() ;
Pour le benchmarking : rjd3toolkit::set_benchmarking().

Exercice

Faire la désaisonnalisation d’une série avec X-13 avec la spécification suivante :

détection automatique du schéma de décomposition, des outliers et du modèle ARIMA ;
une correction des jours ouvrables “working days” et un effet graduel de Pâques.

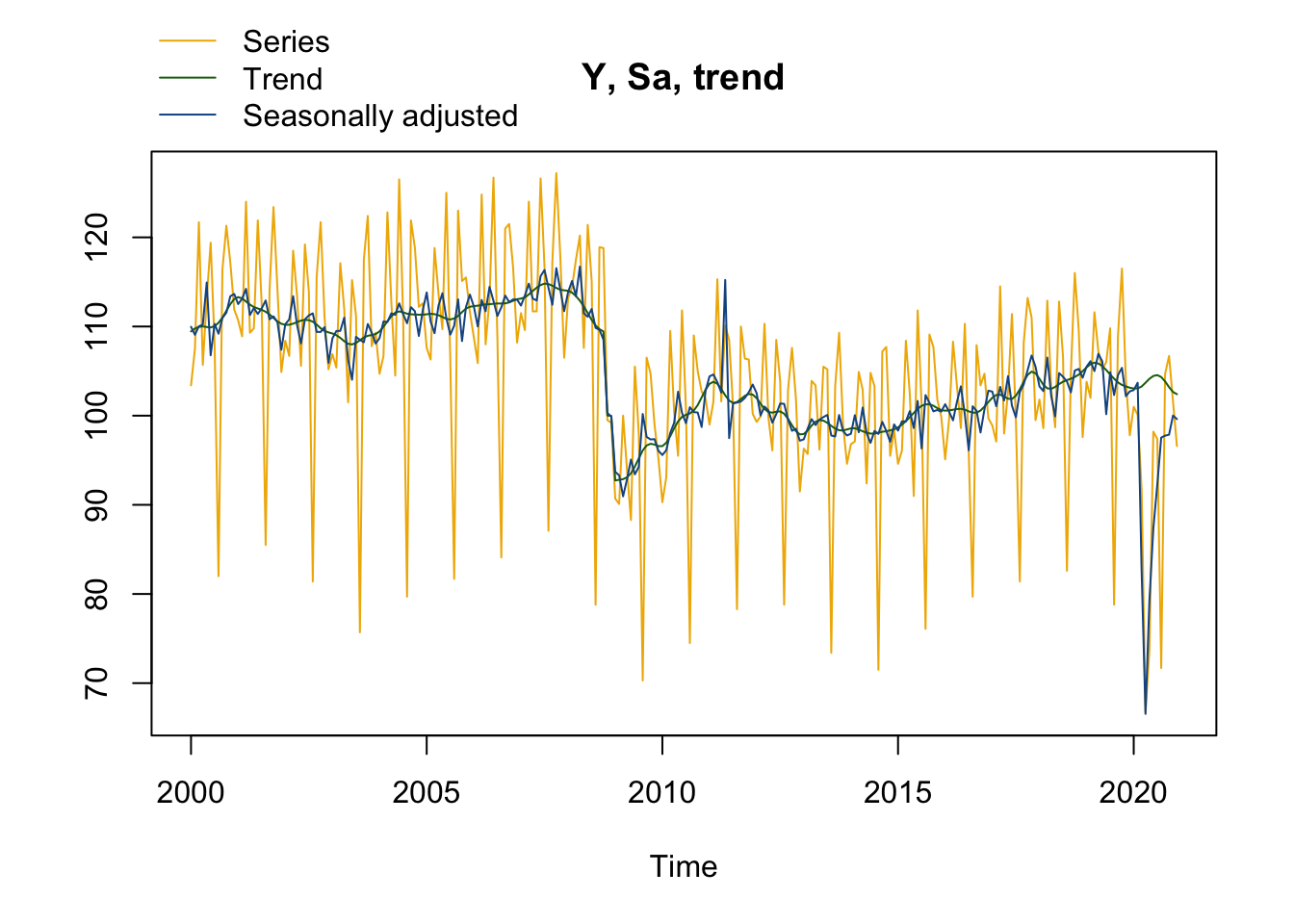
Faire ensuite un graphique avec la série brute et la série désaisonnalisée.

Indice

Utiliser la spécification RSA4 pour la désaisonnalisation.

Si le modèle créé s’appelle sa_jd3, regarder les valeurs de sa_jd3$result$final et rjd3toolkit::sa_decomposition(sa_jd3).

Solution

sa_jd3 <- rjd3x13::x13(RJDemetra::ipi_c_eu[, "FR"], "rsa4")
sa_jd3

Model: X-13
Log-transformation: no 
SARIMA model: (2,1,1) (0,1,1)

SARIMA coefficients:
   phi(1)    phi(2)  theta(1) btheta(1) 
  0.05291   0.18672  -0.52138  -0.66132 

Regression model:
             td              lp          easter LS (2008-11-01) LS (2009-01-01) 
         0.6927          2.0903         -2.5476         -9.2744         -7.2838 
AO (2011-05-01) AO (2020-03-01) TC (2020-04-01) 
        13.1870        -21.1492        -35.6481 

 Seasonal filter: S3X3;  Trend filter: H-13 terms
 M-Statistics: q Good (0.355); q-m2 Good (0.389)
 QS test on SA: Good (0.924);  F-test on SA: Good (0.632)

For a more detailed output, use the 'summary()' function.

y <- sa_jd3$result$preadjust$a1
sa <- sa_jd3$result$final$d11final
# ou :
decomp <- rjd3toolkit::sa_decomposition(sa_jd3)
y <- decomp$series
sa <- decomp$sa
# ou on peut directement utiliser les fonctions de rjd3x13 :
plot(sa_jd3, first_date = 2000 #Pour n'afficher le graphique qu'à partir de 200
)

Pour des graphiques ggplot2, on peut également utiliser le package ggdemetra3.

Exercice

Modifier le modèle précédent pour enlever l’effet graduel de Pâques.

Solution

spec_sans_easter_v3 <- 
    sa_jd3$estimation_spec |> 
    rjd3toolkit::set_easter(enabled = FALSE)
sa2_jd3 <- rjd3x13::x13(RJDemetra::ipi_c_eu[, "FR"], spec_sans_easter_v3)
sa2_jd3$result$preprocessing

Log-transformation: no 
SARIMA model: (2,1,1) (0,1,1)

SARIMA coefficients:
   phi(1)    phi(2)  theta(1) btheta(1) 
  0.02527   0.10075  -0.59512  -0.71292 

Regression model:
             td              lp LS (2008-11-01) AO (2011-05-01) AO (2020-03-01) 
         0.7032          2.1641        -12.7560         13.1047        -20.3006 
TC (2020-04-01) 
       -36.4048 

For a more detailed output, use the 'summary()' function.

Exercice

Calculer les p-valeurs associées au modèle Reg-ARIMA de la précédente spécification.

Indice

Récupérer le modèle Reg-ARIMA et utiliser la fonction summary().

Solution

summary(sa2_jd3$result$preprocessing)

Log-transformation: no 
SARIMA model: (2,1,1) (0,1,1)

Coefficients
          Estimate Std. Error  T-stat Pr(>|t|)    
phi(1)     0.02527    0.09998   0.253    0.801    
phi(2)     0.10075    0.07425   1.357    0.176    
theta(1)  -0.59512    0.08863  -6.715 7.65e-11 ***
btheta(1) -0.71292    0.04618 -15.439  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Regression model:
                 Estimate Std. Error  T-stat Pr(>|t|)    
td                0.70321    0.03417  20.582  < 2e-16 ***
lp                2.16412    0.76568   2.826  0.00498 ** 
LS (2008-11-01) -12.75601    1.66740  -7.650 1.99e-13 ***
AO (2011-05-01)  13.10471    1.97806   6.625 1.32e-10 ***
AO (2020-03-01) -20.30056    2.25944  -8.985  < 2e-16 ***
TC (2020-04-01) -36.40477    2.19426 -16.591  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Number of observations: 372, Number of effective observations: 359, Number of parameters: 11
Loglikelihood: -817.6149
Standard error of the regression (ML estimate): 2.330069 
AIC: 1657.23, AICc: 1657.991, BIC: 1699.946

2 Créer un workspace

Dans cette partie nous allons créer un workspace depuis R. Pour cela les fonctions qui peuvent être utilisées sont rjd3workspace::jws_new(), rjd3workspace::read_workspace(), rjd3workspace::jws_sap_new(), rjd3workspace::add_sa_item(), rjd3workspace::save_workspace().

Exercice

Créer un workspace qui va contenir une série désaisonnalisée selon 3 spécifications différentes.

Solution

jws <- rjd3workspace::jws_new()
jsap <- rjd3workspace::jws_sap_new(jws, "MP-1")
rjd3workspace::add_sa_item(jsap, "X13 avec Pâques", sa_jd3)
rjd3workspace::add_sa_item(jsap, "X13 sans Pâques", sa2_jd3)
rjd3workspace::add_sa_item(jsap, "TRAMO-SEATS", y, rjd3tramoseats::spec_tramoseats())
rjd3workspace::save_workspace(jws, "ws_v3.xml")

Exercice

Importer le workspace précédent et récupérer :

Le nom du premier multi-processing
Le nombre de modèles dans ce premier multi-processing
L’ensemble des séries brutes
Le 2ème modèle

Solution

# charge tous les modèles du workspace :
jws <- rjd3workspace::.jws_open("ws_v3.xml")
ws <- rjd3workspace::read_workspace(jws)
names(ws$processing)[1]

[1] "MP-1"

length(ws$processing[[1]]) # Nombre de multiprocessing

[1] 3

Autre façon de faire similaire à RJDemetra :

# charge tous les modèles du workspace :
jws <- rjd3workspace::.jws_open("ws_v3.xml")
rjd3workspace::jws_compute(jws)
rjd3workspace::ws_sap_count(jws) # Nombre de multiprocessing

[1] 1

jsap1 <- rjd3workspace::jws_sap(jws, 1) # Le premier multiprocessing
rjd3workspace::sap_name(jsap1)

[1] "MP-1"

rjd3workspace::sap_sai_count(jsap1)

[1] 3

model2 <- rjd3workspace::jsap_sai(jsap1, 2) # On récupère l'objet associé au 2ème modèle
rjd3workspace::read_sai(model2)

$ts
$name
[1] "X13 sans Pâques"

$moniker
$source
[1] ""

$id
[1] "54564427-00d3-498b-bbd1-2c745e88e096"

attr(,"class")
[1] "JD3_TSMONIKER"

$metadata
NULL

$data
       Jan   Feb   Mar   Apr   May   Jun   Jul   Aug   Sep   Oct   Nov   Dec
1990  92.1  92.3 102.1  93.0  93.3 100.8  92.9  66.7  95.8 105.0  96.7  89.2
1991  92.5  89.2  97.4  93.8  87.5 100.3  93.4  64.3  96.9 103.5  94.0  92.1
1992  90.7  89.0  99.4  93.7  86.1 101.3  90.4  62.9  96.6  98.4  91.9  92.6
1993  82.3  84.0  95.6  88.3  82.2  97.9  85.5  61.3  93.7  93.0  88.3  92.1
1994  83.6  83.7  97.0  88.3  88.3 102.9  87.3  65.9  98.2  98.0  96.8  98.0
1995  91.8  90.1 102.9  90.4  91.6 103.7  90.6  66.8  98.7 101.4  97.2  94.8
1996  92.0  91.1  98.1  94.3  90.5 101.8  96.1  66.3  98.9 105.0  95.0  96.0
1997  91.9  91.3  99.1 102.8  93.2 108.2 100.4  70.5 107.3 114.1  99.6 106.7
1998  98.2  98.7 109.3 103.7  97.6 114.7 106.1  72.1 111.5 112.6 105.6 107.4
1999  97.2  98.3 114.5 104.8  99.9 120.2 105.7  76.1 115.2 115.1 111.1 114.0
2000 103.4 107.5 121.7 105.7 113.1 119.4 108.1  82.0 116.4 121.3 117.2 111.9
2001 110.7 108.9 124.0 109.3 109.8 121.9 112.4  85.5 114.1 123.4 114.2 104.9
2002 108.4 106.7 118.5 113.4 105.6 119.2 113.9  81.4 115.6 121.7 111.0 105.2
2003 106.9 105.4 117.1 112.0 101.5 115.2 111.2  75.7 117.5 122.4 107.8 109.3
2004 104.7 106.7 122.8 112.7 104.5 126.5 111.1  79.7 121.9 118.8 112.2 112.6
2005 107.6 106.3 118.8 113.7 109.7 125.0 106.4  81.7 123.0 115.1 115.5 111.6
2006 108.8 105.9 124.8 108.0 113.1 126.7 108.7  84.1 121.0 121.5 116.6 108.2
2007 111.5 109.6 124.0 111.7 111.7 126.6 116.6  87.1 117.3 127.2 118.0 106.5
2008 113.2 114.4 117.5 120.2 107.6 121.4 115.1  78.8 118.9 118.8  99.5  99.2
2009  90.7  90.1 100.0  93.9  88.3 105.5  97.9  70.3 106.5 104.7  99.0  95.2
2010  90.3  93.1 109.5 100.4  95.5 111.8 100.8  74.5 109.0 105.0 102.7 101.9
2011  99.0 101.6 115.3 101.6 110.1 108.5 101.0  78.3 110.0 106.4 106.3 100.2
2012  99.3  99.9 110.3  99.8  96.1 108.5 103.8  78.8 102.9 107.6 101.9  91.5
2013  96.3  95.7 103.9 103.4  96.2 105.5 105.2  73.4 103.3 109.3  99.0  94.6
2014  96.8  97.1 104.9 102.9  92.4 104.8 103.3  71.5 107.2 107.7  95.5  98.4
2015  94.6  96.1 108.4 102.4  91.0 111.8 101.1  76.1 109.1 107.7 101.8  99.9
2016  95.1  99.6 108.3 103.3  98.6 110.3  95.8  79.7 107.9 103.4 104.7  99.7
2017  98.9  97.1 114.5  98.0 102.7 111.4  99.5  81.4 108.2 113.2 111.0  99.5
2018 101.8  98.6 112.9 103.0  98.7 112.8 106.6  82.6 104.7 116.0 109.6  97.6
2019 103.8 102.0 111.6 107.2 105.2 106.0 109.8  78.8 109.0 116.5 104.0  97.8
2020 101.0 100.1  91.8  66.7  73.7  98.2  97.4  71.7 104.7 106.7 101.6  96.6

attr(,"class")
[1] "JD3_TS"

$domainSpec
Specification

Series
Serie span: All 
Preliminary Check: Yes

Estimate
Model span: All 

Tolerance: 1e-07

Transformation
Function: AUTO
AIC difference: -2
Adjust: NONE

Regression
Calendar regressor: WorkingDays
with Leap Year: Yes
AutoAdjust: TRUE
Test: REMOVE

Easter: No

Pre-specified outliers: 0
Ramps: No

Outliers
Detection span: All 
Outliers type: 
    - AO, critical value : 0 (Auto)
    - LS, critical value : 0 (Auto)
    - TC, critical value : 0 (Auto)
TC rate: 0.7 (Auto)
Method: ADDONE (Auto)

ARIMA
SARIMA model: (0,1,1) (0,1,1)

SARIMA coefficients:
 theta(1) btheta(1) 
        0         0 

Specification X11
Seasonal component: Yes
Length of the Henderson filter: 0
Seasonal filter: FILTER_MSR
Boundaries used for extreme values correction : 
     lower_sigma:  1.5 
     upper_sigma:  2.5
Nb of forecasts: -1
Nb of backcasts: 0
Calendar sigma: NONE

Benchmarking
Is enabled: No

$estimationSpec
Specification

Series
Serie span: All 
Preliminary Check: Yes

Estimate
Model span: All 

Tolerance: 1e-07

Transformation
Function: AUTO
AIC difference: -2
Adjust: NONE

Regression
Calendar regressor: WorkingDays
with Leap Year: Yes
AutoAdjust: TRUE
Test: REMOVE

Easter: No

Pre-specified outliers: 0
Ramps: No

Outliers
Detection span: All 
Outliers type: 
    - AO, critical value : 0 (Auto)
    - LS, critical value : 0 (Auto)
    - TC, critical value : 0 (Auto)
TC rate: 0.7 (Auto)
Method: ADDONE (Auto)

ARIMA
SARIMA model: (0,1,1) (0,1,1)

SARIMA coefficients:
 theta(1) btheta(1) 
        0         0 

Specification X11
Seasonal component: Yes
Length of the Henderson filter: 0
Seasonal filter: FILTER_MSR
Boundaries used for extreme values correction : 
     lower_sigma:  1.5 
     upper_sigma:  2.5
Nb of forecasts: -1
Nb of backcasts: 0
Calendar sigma: NONE

Benchmarking
Is enabled: No

$pointSpec
Specification

Series
Serie span: All 
Preliminary Check: Yes

Estimate
Model span: All 

Tolerance: 1e-07

Transformation
Function: LEVEL
AIC difference: -2
Adjust: NONE

Regression
Calendar regressor: WorkingDays
with Leap Year: Yes
AutoAdjust: FALSE
Test: NO

Easter: No

Pre-specified outliers: 4
    - LS (2008-11-01), coefficient: -12.7560067943903 (ESTIMATED)
    - AO (2011-05-01), coefficient: 13.1047116166881 (ESTIMATED)
    - AO (2020-03-01), coefficient: -20.3005616124476 (ESTIMATED)
    - TC (2020-04-01), coefficient: -36.4047650490134 (ESTIMATED)
Ramps: No

Outliers
Is enabled: No

ARIMA
SARIMA model: (2,1,1) (0,1,1)

SARIMA coefficients:
   phi(1)    phi(2)  theta(1) btheta(1) 
  0.02527   0.10075  -0.59512  -0.71292 

Specification X11
Seasonal component: Yes
Length of the Henderson filter: 0
Seasonal filter: FILTER_MSR
Boundaries used for extreme values correction : 
     lower_sigma:  1.5 
     upper_sigma:  2.5
Nb of forecasts: -1
Nb of backcasts: 0
Calendar sigma: NONE

Benchmarking
Is enabled: No

$results
Model: X-13
Log-transformation: no 
SARIMA model: (2,1,1) (0,1,1)

SARIMA coefficients:
   phi(1)    phi(2)  theta(1) btheta(1) 
  0.02527   0.10075  -0.59512  -0.71292 

Regression model:
             td              lp LS (2008-11-01) AO (2011-05-01) AO (2020-03-01) 
         0.7032          2.1641        -12.7560         13.1047        -20.3006 
TC (2020-04-01) 
       -36.4048 

 Seasonal filter: S3X3;  Trend filter: H-13 terms
 M-Statistics: q Good (0.316); q-m2 Good (0.346)
 QS test on SA: Good (1.000);  F-test on SA: Good (0.646)

For a more detailed output, use the 'summary()' function.

# Pour extraire toutes les séries brutes il faut faire une boucle :
all_y <- lapply(
    lapply(
        seq_len(rjd3workspace::sap_sai_count(jsap1)),
        rjd3workspace::.jsap_sai, jsap = jsap1
    ),
    rjd3workspace::get_raw_data
)

3 Manipuler les objets Java

La manipulation des objets Java se fait de la même façon qu’avec RJDemetra : .jx13() pour estimer les modèles (nom de la fonction légèrement différente), rjd3toolkit::dictionary() pour connaitre l’ensemble des objets exportables et rjd3toolkit::result() et rjd3toolkit::user_defined() pour exporter des objets.

Exercice

Créer un modèle à partir de la fonction .jx13() et la spécification sans effet graduel de pâques calculée dans la section 1.

Solution

myjsa <- rjd3x13::.jx13(RJDemetra::ipi_c_eu[, "FR"], spec_sans_easter_v3)
rjd3toolkit::result(myjsa, "sa")

           Jan       Feb       Mar       Apr       May       Jun       Jul
1990  93.24955  95.30940  94.71796  93.81684  93.54929  92.92520  94.21426
1991  93.59169  92.31215  92.64331  92.17822  87.64814  94.71770  92.26714
1992  91.58585  91.95491  92.44861  92.08835  91.15320  90.56855  89.24060
1993  87.99561  87.69727  86.39964  86.75333  87.31361  86.83199  86.72062
1994  89.29811  87.67745  87.97237  89.30396  91.16780  91.47286  90.78785
1995  95.25155  94.23926  93.90860  94.00837  92.19870  91.94726  93.82107
1996  93.17973  92.48812  93.89705  93.13793  91.31516  94.72025  94.11951
1997  93.26078  95.70964  94.51600 101.81259  96.59510  98.42946  98.22737
1998 102.21091 103.17118 101.63558 102.93616 103.62068 102.28550 103.77953
1999 103.79658 102.78743 103.69074 104.14106 106.09004 107.66846 105.67101
2000 110.10497 109.06807 110.12489 109.82704 114.79035 106.77270 110.36351
2001 112.60460 113.23756 114.26231 110.62978 111.90510 111.50689 112.11052
2002 110.38323 110.96526 110.79945 111.78627 107.92165 110.99153 111.32654
2003 108.79624 109.74015 109.32134 109.98806 106.03352 104.23265 108.95547
2004 108.85117 110.81356 110.13728 110.54560 111.16466 112.78890 111.54538
2005 113.93316 110.84172 106.41816 114.18867 113.55450 111.11371 109.26845
2006 112.42833 110.33885 112.86559 111.31529 114.27002 113.01129 111.32242
2007 112.55694 113.84939 115.05181 112.93951 112.66924 115.79095 116.41635
2008 114.19262 115.43079 111.37148 119.20887 111.21601 111.20490 111.96753
2009  94.06595  93.66765  91.59029  92.93345  94.74414  93.45541  94.24009
2010  96.01716  96.45680  98.71937  99.12528 102.35680 100.33373  99.14123
2011 104.73308 104.88254 104.41611 102.25226 114.86761  97.50904 101.41146
2012 102.69646 100.10116 101.67631  99.91395  98.94360 100.23048 101.39058
2013  97.38049  98.67284  97.59268 100.48330  99.43876  99.96091 100.12816
2014  98.00446 100.13410  98.51684  99.69373  98.14253  97.00824  98.38996
2015  98.43075  99.49303  99.43229  99.18875  98.89465 101.71133  96.50599
2016 101.43553 100.46907  96.73895 102.94029 103.57872 100.21169  96.40288
2017 102.83484 101.21980 102.93078 100.60288 104.65915 101.21299 100.09477
2018 103.34498 102.86547 103.87513 103.61900 100.09104 104.87134 104.57061
2019 105.55319 106.23769 105.20469 105.62380 106.14533 100.29916 105.00063
2020 102.89360 103.74645  83.07039  65.24951  79.29577  87.38128  92.35517
           Aug       Sep       Oct       Nov       Dec
1990  92.38173  93.51234  93.42343  92.18042  90.41279
1991  92.42873  92.22349  92.01173  92.00186  90.59538
1992  93.45078  89.51221  89.56165  89.95835  88.19546
1993  89.35917  86.63394  86.80871  84.00049  87.21539
1994  91.47220  91.08205  91.83094  92.70377  95.22430
1995  92.43935  93.94802  92.67708  93.29762  94.39315
1996  94.63683  93.94307  93.57709  93.75204  93.25425
1997 101.68755  99.71695 102.44668 100.79734 101.82217
1998 103.67043 103.81100 103.12842 104.36147 102.98643
1999 105.51412 107.47894 108.01349 107.32689 110.17856
2000 109.19601 111.03577 111.63442 113.48334 113.71019
2001 112.97886 110.95332 111.23200 110.59473 107.49517
2002 111.59373 109.55119 109.54524 110.06801 106.01718
2003 108.67882 108.40221 110.46920 109.44340 108.13524
2004 110.49903 112.36423 111.93619 108.93019 111.82427
2005 110.17307 113.24026 108.51104 112.00879 113.43584
2006 112.19306 113.67537 112.74018 112.68488 112.70890
2007 114.35913 112.60498 116.41114 113.72338 111.21506
2008 109.87755 109.64124 108.31326  99.94885  99.31443
2009 100.20028  97.57161  97.15487  97.05587  95.50465
2010 100.91566 100.33425 100.28702  98.54035 102.42445
2011 101.41452 101.52787 102.02302 102.59491 103.34800
2012 101.29425  99.61270  98.34668  98.61297  97.28502
2013  97.82035  97.74060 100.19255  98.38971  97.85776
2014  98.04534  99.36208  98.45915  97.19073  99.09353
2015 102.42001 101.51956 100.68665 100.72423 100.52605
2016 101.09905 100.59846  98.34729 100.76466 102.91719
2017 102.74040 103.61311 105.30626 106.79695 105.62276
2018 103.94813 102.71388 105.22599 105.29463 104.37228
2019 102.51548 104.62023 105.52898 102.28202 102.79014
2020  97.79844  97.77412  98.09488 100.12642  99.63962

Pour les révisions, la fonction rjd3x13::x13_revisions() facilite grandement la tâche. L’historique des révisions peut s’exporter à partir de trois paramètres :

data_ids qui permet d’exporter des statistiques ;
ts_ids qui permet d’exporter des estimations d’une composante à une certaine date ;
cmp_ids qui permet l’ensemble des estimations d’une composante à une ensemble de dates.

data_ids <- list(
    # Export du coefficient du premier régresseur jours ouvrables
    list(start = "2005-01-01", id = "regression.td(1)"))
ts_ids <- list(
    # Export de l'historique des estimations de la séries SA de janv 2010 à partir de janvier 2010
    list(period = "2010-01-01", start = "2010-01-01", id = "sa"))
cmp_ids <- list(
    # Export de l'ensemble des tendances estimées entre janv 2010 et dec 2014
    list(start = "2010-01-01", end = "2014-12-01", id = "t"))
rh <- rjd3x13::x13_revisions(
    sa2_jd3$result$preadjust$a1,
    spec = sa2_jd3$result_spec, 
    data_ids, ts_ids, cmp_ids)
plot(rh$data$`regression.td(1)`,
     ylab = "Coef", main = "Coef td")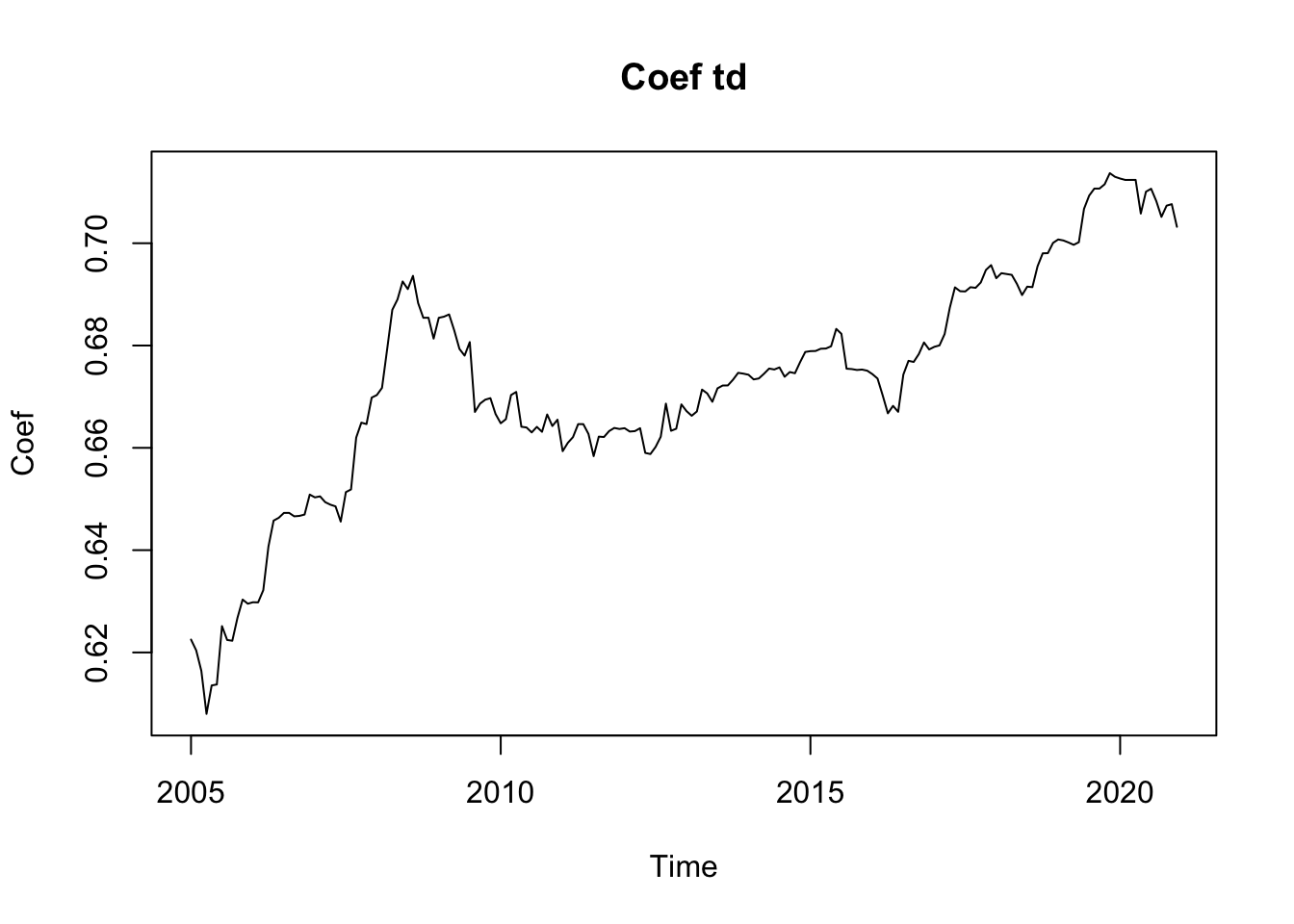

plot(rh$series$sa,
     ylab = NULL, main = "SA de janv 2010")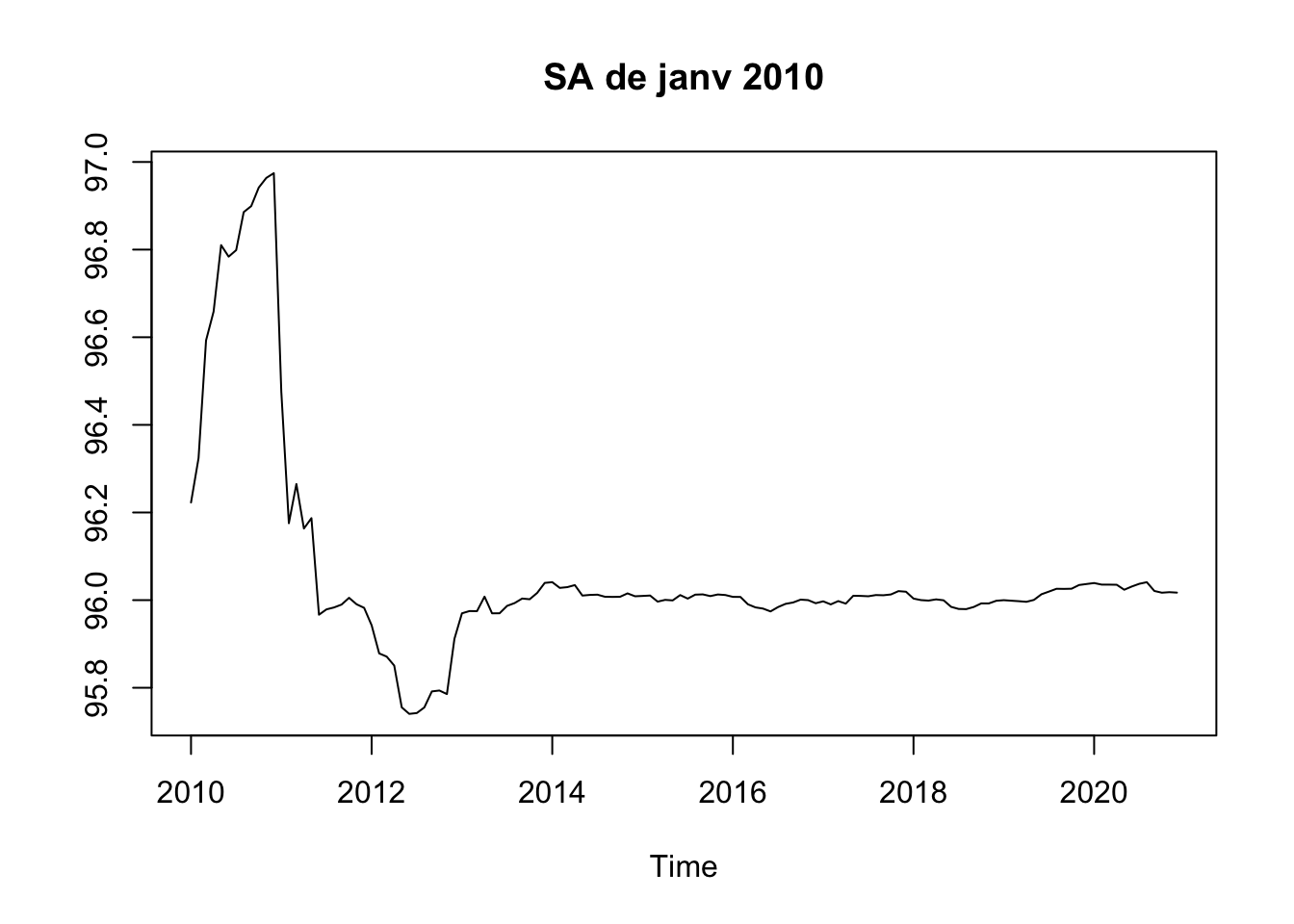

ncol(rh$components$t) # nombre de séries exportées

[1] 60