packages_to_install <- c("forecast", "ggplot2", "plotly")
packages <- packages_to_install[! packages_to_install %in% installed.packages()[,"Package"]]
if (length(packages) > 0) {
install.packages(packages)
}
packages_to_install_git <- c("rjd3toolkit", "rjd3highfreq", "rjd3filters", "rjd3x11plus")
packages_git <- packages_to_install_git[! packages_to_install_git %in% installed.packages()[,"Package"]]
if (length(packages_git) > 0) {
# # Configurer si besoin le proxy
# proxy <- "proxy_a_definir"
# Sys.setenv(HTTPS_PROXY = proxy)
remotes::install_github(
sprintf("rjdemetra/%s", packages_git),
# option utile dans certaines installations portables de Java :
INSTALL_opts = "--no-multiarch")
}
if (! "ggdemetra3" %in% installed.packages()[,"Package"])
remotes::install_github("AQLT/ggdemetra3")6 - Désaisonnalisation à haute-fréquence
Désaisonnaliser une série temporelle
L’objectif de ce TP est de montrer un exemple de désaisonnalisation de séries haute-fréquence.
Pour installer tous les packages utiles de ce TP, lancer le programme :
Nous utiliserons la base forecast::taylor de demande d’électricité par demi-heure en Angleterre et au Pays de Galles du lundi 5 juin 2000 au dimanche 27 août 2000.
library(rjd3highfreq)
library(forecast)
library(plotly)
library(ggplot2)
trace_ch <- function(x, p0, p1, np= p1 - p0 + 1, original = TRUE, interactive = FALSE) {
sa_tests <- rjd3toolkit::seasonality_canovahansen(
x,
p0 = p0, p1 = p1, np = np,
original = original)
x <- seq.int(from = p0, length.out = length(sa_tests))
if (interactive) {
plot_ly() |>
add_trace(
type = "scatter",
mode = "lines",
x = x,
y = sa_tests
)
} else {
plot(x, sa_tests, type = "l")
}
}
graph_comp <- function(data) {
dataGraph <- reshape2::melt(data, id="x")
ggplot(data = dataGraph, aes(x = x, y = value, color = variable)) +
geom_line()
}
x <- seq(as.POSIXct("2020-06-05 00:00:00"), as.POSIXct("2020-08-27 23:30:00"), by="30 min")La saisonnalité est clairement identifiable sur la série brute :
plot(x, taylor, type = "l")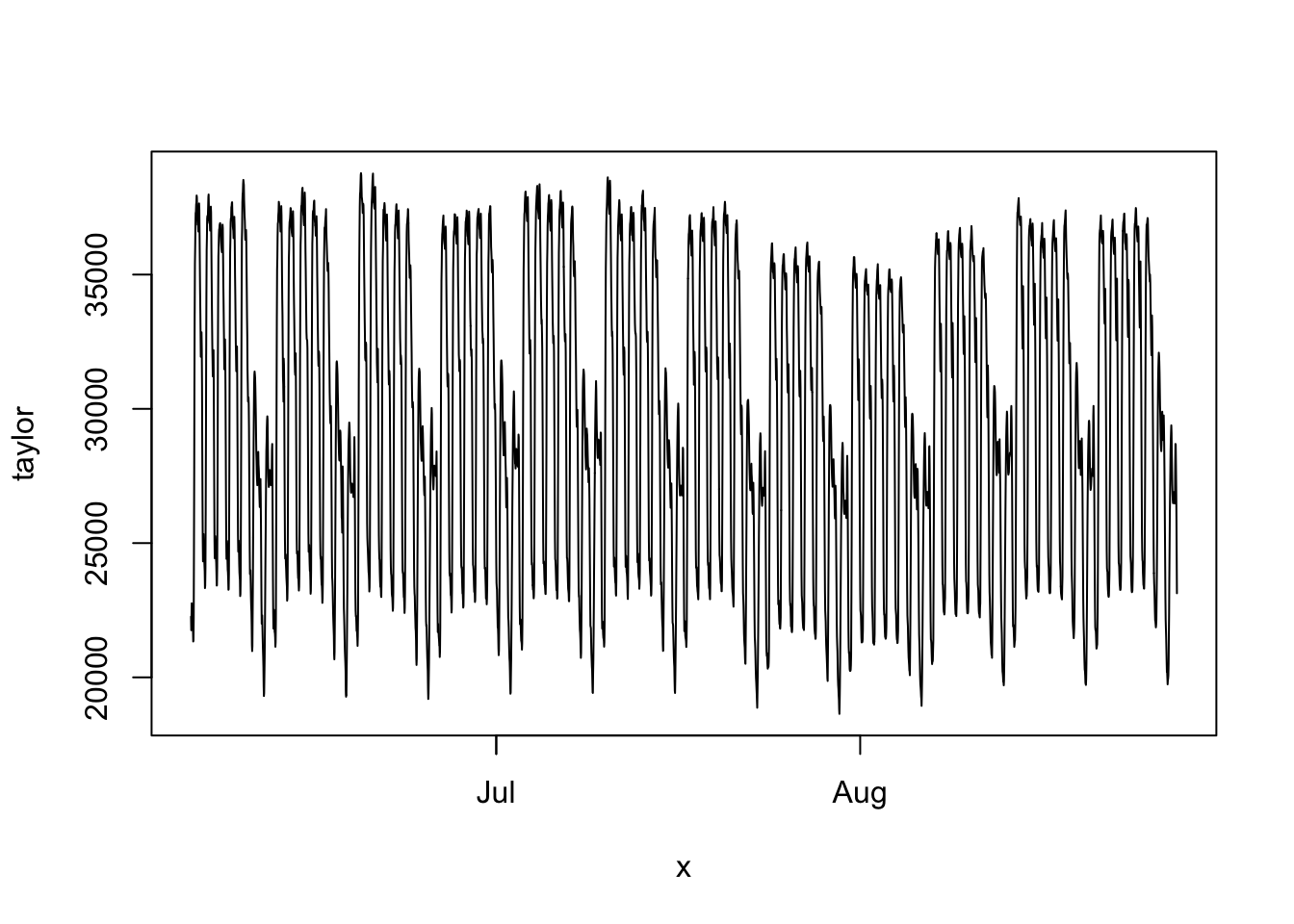
On peut effectuer un test pour Canova-Hansen pour le vérifier :
trace_ch(taylor, p0 = 2, p1 = 2*24*7, np = 2*24*7-1)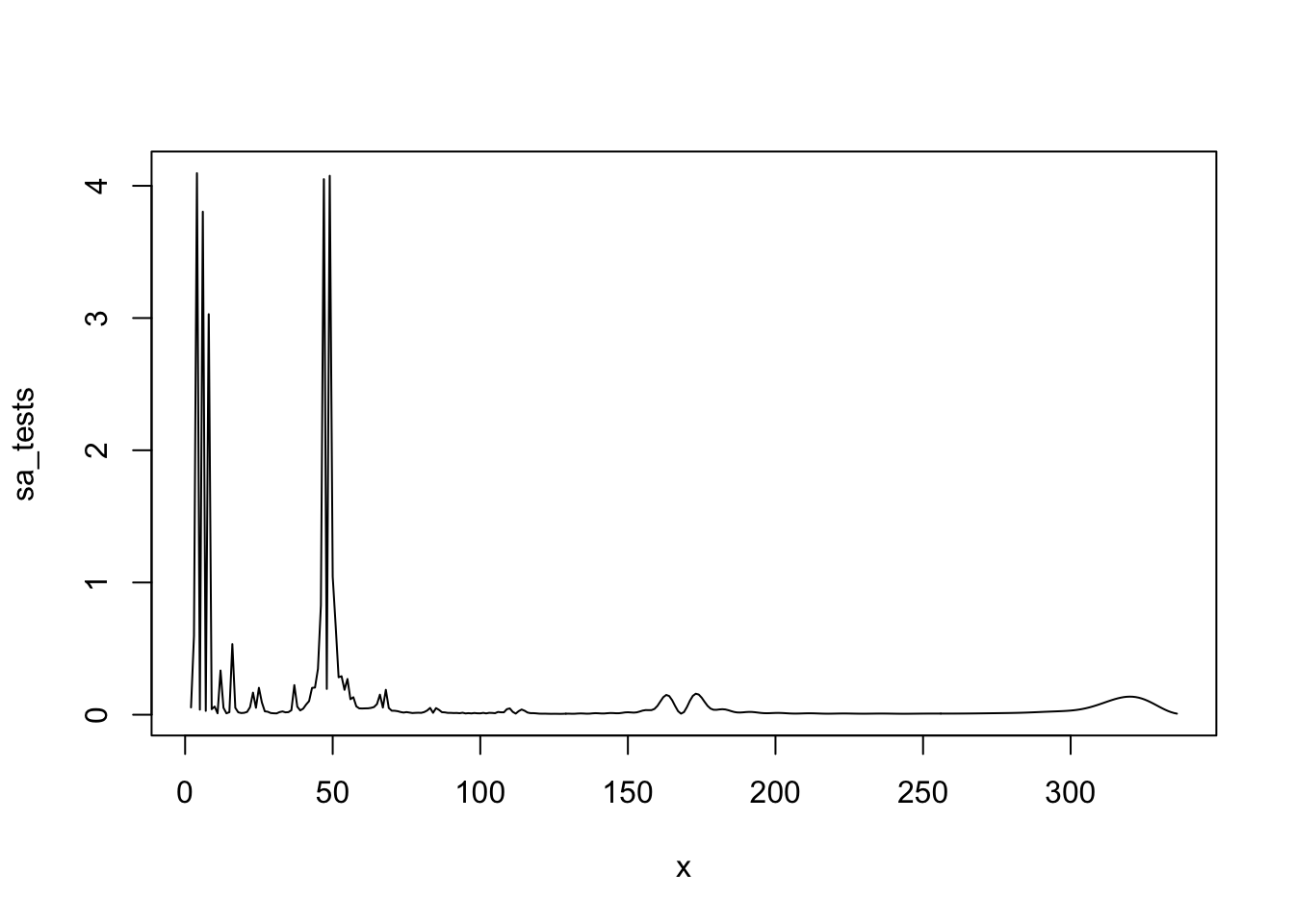
On observe deux pics, pour des périodicités faibles (horaire ? cela ne s’explique pas) et autour de 48 (saisonnalité journalière). En faisant une différenciation journalière, on remarque qu’il reste de la saisonnalité qui est hebdomadaire (\(2\times24\times7\)) :
plot(x[-(1:48)], rjd3toolkit::differences(taylor, 48), type = "l")
lines(x[-(1:48)][-(1:(2*24*7))], rjd3toolkit::differences(taylor, c(48, 2*24*7)), col = "red")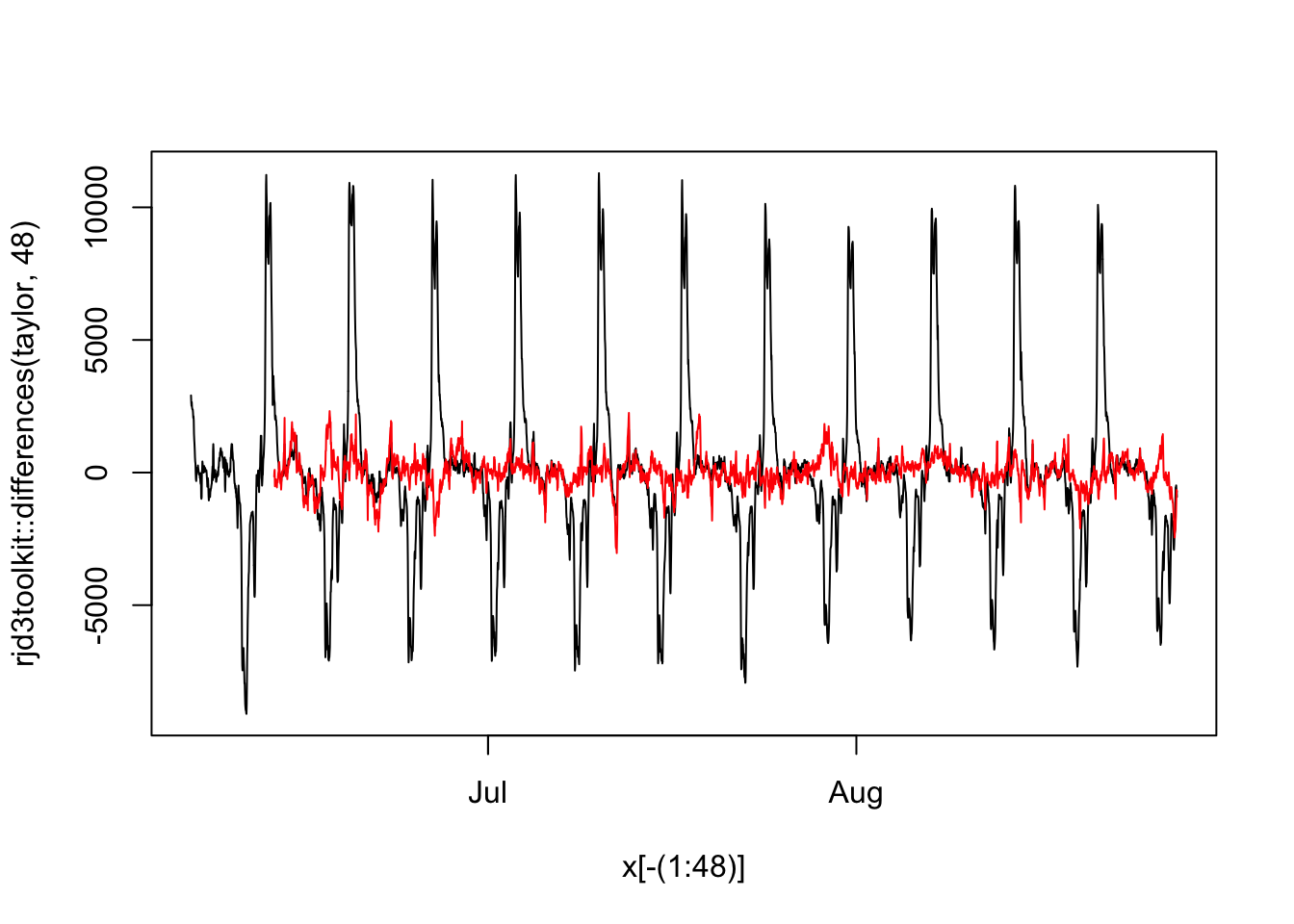
La première méthode que nous utiliserons est la méthode mSTL. Elle prend en entrée des objets msts qui peuvent être créés avec la fonction forecast::msts() pour spécifier les différentes saisonnalités. Ici la base taylor est déjà au bon format mais on aurait pu la créer avec le code msts(taylor, seasonal.periods = c(2 * 24, 2*24*7)).
mstl_mod <- mstl(taylor,)
autoplot(mstl_mod)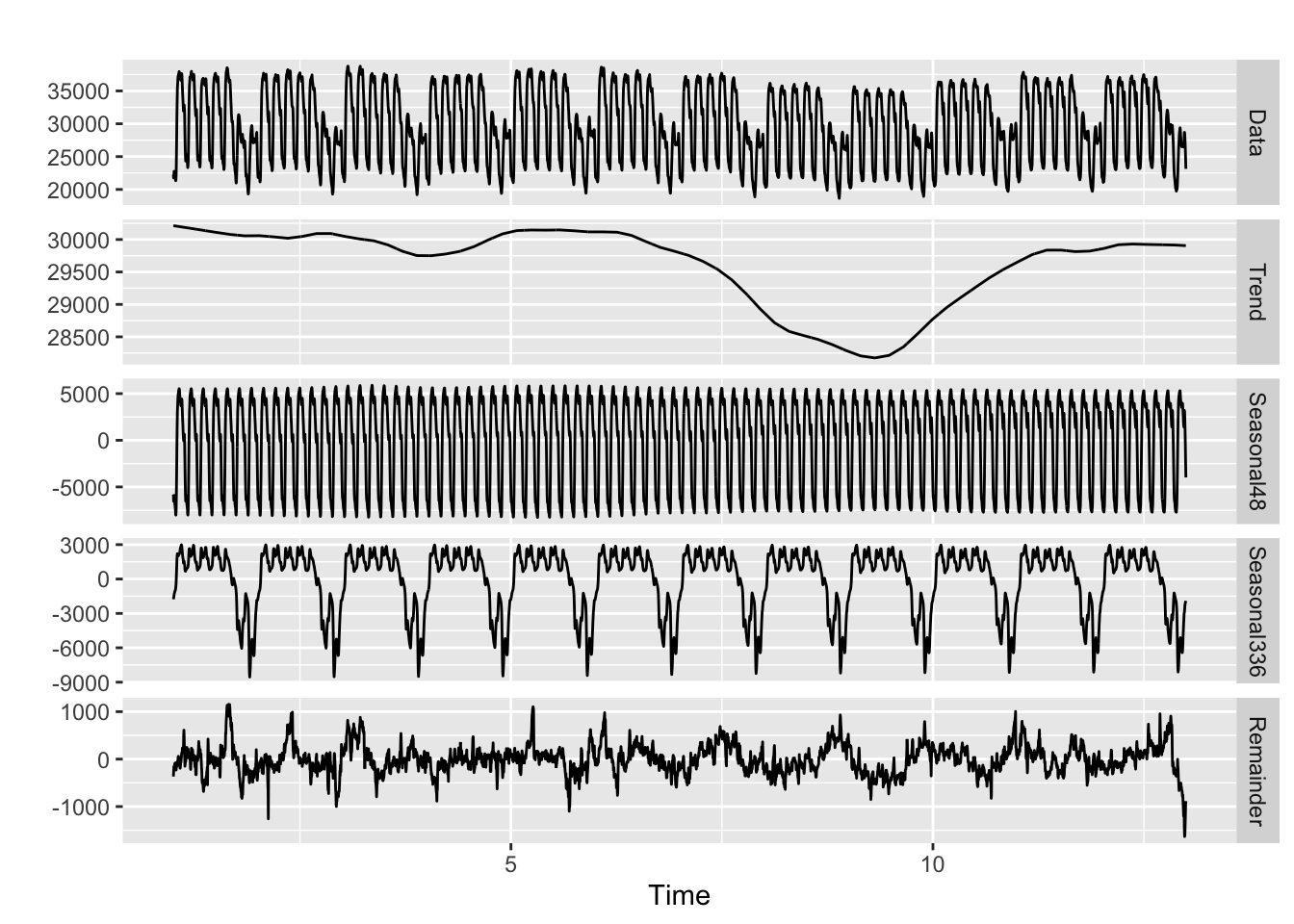
Par défaut, une moyenne mobile de longueur 11 est utilisée pour la saisonnalité journalière et de longueur 15 pour la saisonnalité hebdomadaire (paramètre s.window) mais cette hypothèse peut être changée.
On pourrait également estimer le modèle avec TBATS mais le temps de calcul est long et les résultats n’étaient pas satisfaisants. Ci-dessous le code qui pourrait être utilisé :
tbats_mod <- tbats(taylor, seasonal.periods = c(2 * 24, 2*24*7))Utilisons maintenant les méthodes de rjd3highfreq. La série brute est très peu bruitée donc le préajustement n’est pas nécessaire. Par ailleurs pas de tendance marquée et le schéma additif parait adapté :
pre_pro <- fractionalAirlineEstimation(
y = taylor,
periods = c(2*24, 2*24*7),
# pas utile de faire de détection des LS
outliers = c("ao", "wo"),
log = FALSE, y_time = x)
pre_proNumber of observations: 4032
Start: 2020-06-05
End: 2020-08-27 23:30:00
Estimate MA parameters:
MA_parameter Coef Coef_SE Tstat
Theta(1) -0.8100819 0.007010398 -115.55433
Theta(period = 48) 0.3883132 0.020280074 19.14752
Theta(period = 336) 0.7760373 0.018278218 42.45694
Number of calendar regressors: 0 , Number of outliers : 1
Outliers coefficients:
Variable Coef Coef_SE Tstat
AO.2020-06-12 21:00:00 -1234.44 139.3048 -8.8614
Sum of square residuals: 3.063e+08 on 3643 degrees of freedom
Log likelihood = -2.602e+04,
aic = 5.204e+04,
aicc = 5.204e+04,
bic(corrected for length) = 11.35
Hannan–Quinn information criterion = 5.205e+04Il n’y a que 1 point atypique détecté. On va désaisonnaliser la série linéarisée de plusieurs façons : - Désaisonnalisation en deux étapes (journalière puis hebdomadaire) avec rjd3highfreq::fractionalAirlineDecomposition()
Désaisonnalisation en une étape des deux saisonnalités en une étape avec
rjd3highfreq::multiAirlineDecomposition().Désaisonnalisation uniquement de la saisonnalité hebdomadaire.
amb.p1 <- rjd3highfreq::fractionalAirlineDecomposition(
y = pre_pro$model$linearized, # linearized series from preprocessing
period = 2 * 24,
log = FALSE)
# Il reste de la saisonnalité
# plot(ggdemetra3::seasonaladj(amb.p1), type = "l")
# On ajuste maintenant la saisonnalité hebdomadaire :
amb.p2 <- rjd3highfreq::fractionalAirlineDecomposition(
y = amb.p1$decomposition$sa,
period = 2*24*7,
log = FALSE,)
plot(ggdemetra3::seasonaladj(amb.p2), type = "l")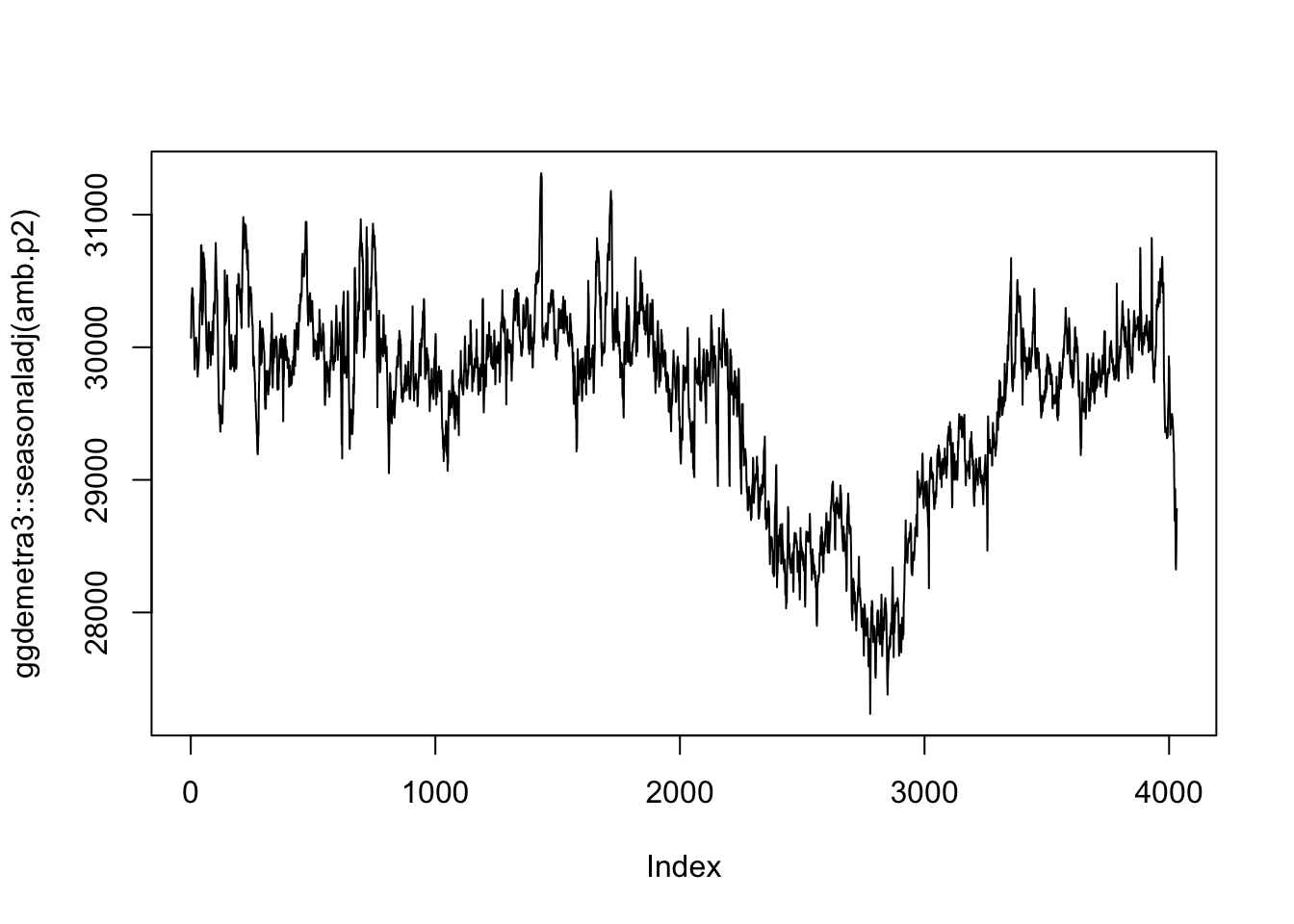
# Si on estime directement la saisonnalité hebdo le résultat semble proche
amb.sem <- rjd3highfreq::fractionalAirlineDecomposition(
y = pre_pro$model$linearized,
period = 2*24*7,
log = FALSE)
amb.multi <- rjd3highfreq::multiAirlineDecomposition(
y = pre_pro$model$linearized,
periods = c(2 * 24, 2*24*7),
log = FALSE, ndiff = 2, y_time = x)Nous allons maintenant construire des tables pour comparer les méthodes. Dans les désaisonnalisations avec rjd3highfreq il faut ajouter les points atypiques du préajustement (pre_pro$model$component_outliers) :
preaj <- pre_pro$model$component_outliers
data_sa <- data.frame(x = x,
# on utilise c() pour enlever le type "msts"
mstl = c(forecast::seasadj(mstl_mod)),
amb_sem = ggdemetra3::seasonaladj(amb.sem) + preaj,
amb_2step = ggdemetra3::seasonaladj(amb.p2) + preaj,
amb_multi = ggdemetra3::seasonaladj(amb.multi) + preaj)
data_t <- data.frame(x = x,
mstl = c(forecast::trendcycle(mstl_mod)),
amb_sem = ggdemetra3::trendcycle(amb.sem),
amb_2step = ggdemetra3::trendcycle(amb.p2),
amb_multi = ggdemetra3::trendcycle(amb.multi))
data_i <- data.frame(x = x,
mstl = c(forecast::remainder(mstl_mod)),
amb_sem = ggdemetra3::irregular(amb.sem) + preaj,
amb_2step = ggdemetra3::irregular(amb.p2) + preaj,
# Ici on récupère i d'une autre façon car petit bug sur la version actuelle
amb_multi = amb.multi$decomposition[[length(amb.multi$decomposition)]] + preaj)
data_s <- data.frame(x = x,
mstl = c(mstl_mod[, "Seasonal48"] + mstl_mod[, "Seasonal336"]),
amb_sem = ggdemetra3::seasonal(amb.sem) ,
amb_2step = ggdemetra3::seasonal(amb.p1) + ggdemetra3::seasonal(amb.p2),
amb_multi = amb.multi$decomposition$s_48 + amb.multi$decomposition$s_336)Les composantes saisonnières sont toutes proches :
graph_comp(data_s)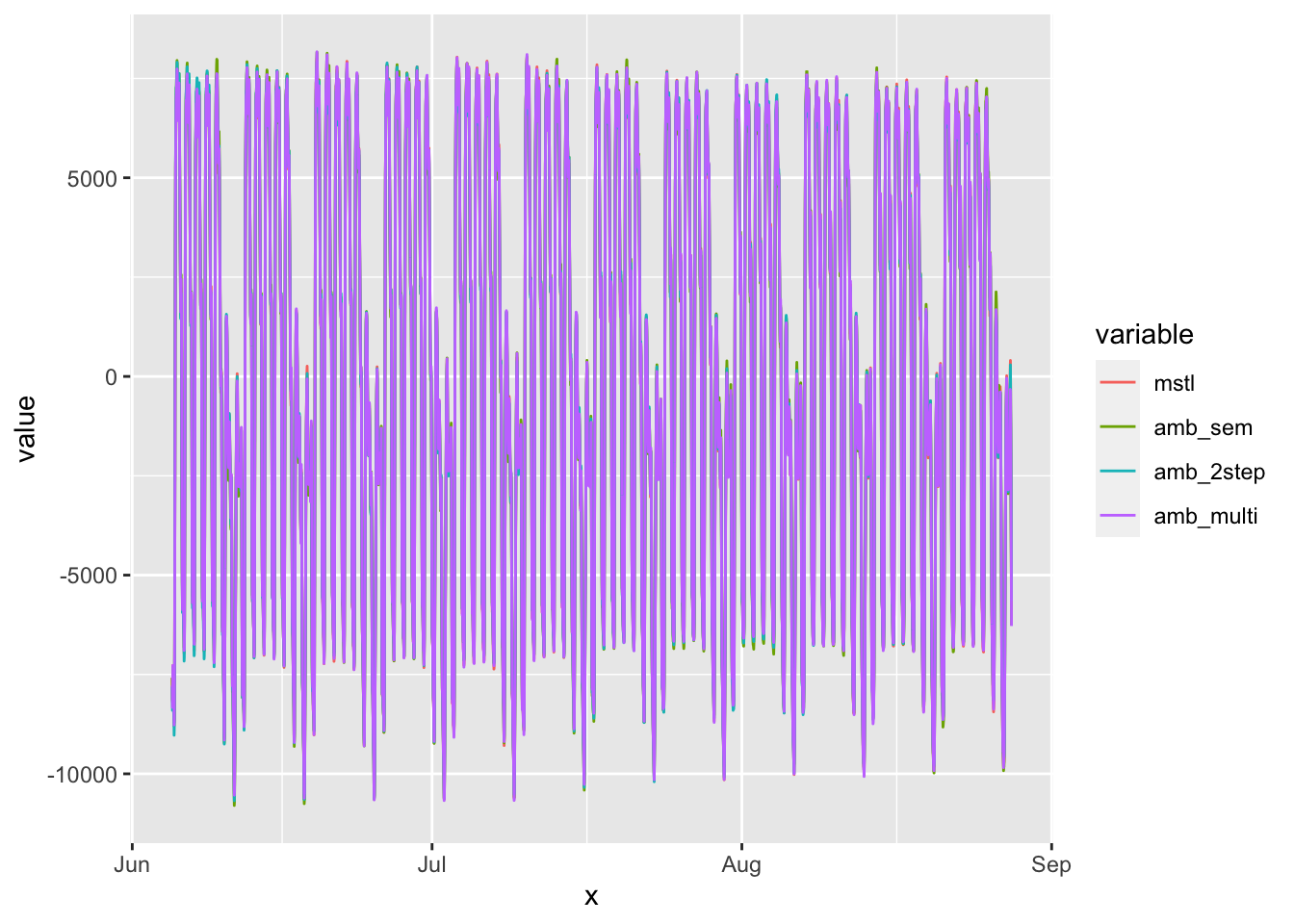
Mais plus de différences sur la tendance et l’irrégulier. La tendance est très erratique avec l’estimation en deux étapes et l’estimation de la saisonnalité hebdomadaire (amb_sem et amb_2step) :
ggplotly(graph_comp(data_t))À part pour le modèle amb_multi, les séries désaisonnalisées semblent proches. On observent notamment plusieurs pics à des fréquences qui semblent journalières ce qui peut amener à penser qu’il faudrait changer les paramètres.
ggplotly(graph_comp(data_sa))