Utilisation de modèles de régression à coefficients variant dans le temps pour la prévision conjoncturelle

Atelier D2E

Auteurs

Claire du Campe de Rosamel

Alain Quartier-la-Tente

Date

16 mars 2023

L’objectif de ce TP est d’apprendre à utiliser quelques fonctionnalités du package tvCoef pour l’estimation de modèles de régression à coefficients variant dans le temps.

Les packages suivants seront utilisés :

packages_to_install <- c("dygraphs", "car", "dynlm")

packages <- installed.packages()[,"Package"][! packages_to_install %in% installed.packages()[,"Package"]]
if (length(packages) > 0) {
    install.packages(packages)
}
if ("tvCoef" %in% installed.packages()[,"Package"]) {
  remotes::install_github("palatej/rjd3toolkit")
  remotes::install_github("palatej/rjd3sts")
  remotes::install_github("AQLT/tvCoef")
}

Pour l’installation de tvCoef, voir le manuel d’installation. Si vous utiliser le https://datalab.ssp.cloud.fr, créer une instance en cliquant ici : .

Pour ce TP nous utiliserons les données de la base tvCoef::manufacturingpour prévoir l’évolution trimestrielle de la production du secteur des autres industries manufacturières (C5, prod_c5) à partir de :

l’acquis de croissance au premier mois du trimestre de l’indice de production industrielle du même secteur (overhang_ipi1_c5) ;
des soldes d’opinion de l’Insee et de la Banque de France. Ces soldes d’opinion sont trimestrialisés en prenant la place du mois dans le trimestre :
- insee_bc_c5_m3 : climat des affaires au 3^e mois du trimestre (mars, juin, septembre, décembre)
- insee_oscd_c5_m2 : niveau des carnets de commandes au 2^e mois du trimestre (février, mai, septembre, novembre)
- insee_tppre_c5_m3 : solde d’opinion sur l’évolution future de la production au 3^e mois du trimestre (février, mai, septembre, novembre).
- bdf_tuc_c5_m2 : taux d’utilisation des capacités de production au deuxième mois du trimestre (février, mai, septembre, novembre).

Les deux dernières variables sont utilisées en différence.

Par simplification, nous estimerons ici le modèle entre le 1993T1 et 2019T4 : pour estimer le modèle au-delà cette date, il faudrait ajouter des indicatrices au cours de l’année 2020 et vérifier si le modèle estimé est toujours bien spécifié.

Le modèle peut alors être estimé en utilisant par exemple la fonction dynlm::dynlm()¹ :

library(tvCoef)
library(dynlm)
data <- window(manufacturing, start = 1993, end = c(2019, 4))
y <- data[, "prod_c5"]
model_c5 <- dynlm(
  formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + insee_oscd_c5_m2
  + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 1),
  data = data
)
model_c5


Time series regression with "ts" data:
Start = 1993(2), End = 2019(4)

Call:
dynlm(formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + 
    insee_oscd_c5_m2 + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 
    1), data = data)

Coefficients:
               (Intercept)            overhang_ipi1_c5  
                 -6.383023                    0.102405  
            insee_bc_c5_m3            insee_oscd_c5_m2  
                  0.061437                   -0.005596  
diff(insee_tppre_c5_m3, 1)      diff(bdf_tuc_c5_m2, 1)  
                  0.039043                    0.397070

Les prévisions dans l’échantillon (in sample) peuvent être extraites avec les fonctions fitted() ou predict() et les prévisions en temps-réel (out of sample) avec la fonction tvCoef::oos_prev().

Pour évaluer la qualité en temps-réel, nous utiliserons les résidus à partir de 2000 :

prev_oos_lm <- oos_prev(model_c5)
res_lm_is <- residuals(model_c5)
res_lm_oos <- prev_oos_lm$residuals
rmse_lm <- c(IS = rmse(res_lm_is), OOS = rmse(res_lm_oos))
rmse_lm

       IS       OOS 
0.6990756 0.8494077

Pour tracer les prévisions, on peut utiliser la fonction plot() :

plot(window(y, start = 2000))
lines(prev_oos_lm$prevision, col = "red")
legend("bottomleft", legend = c("y","Prev. temps réel"),
       col= c("black", "red"), lty = 1)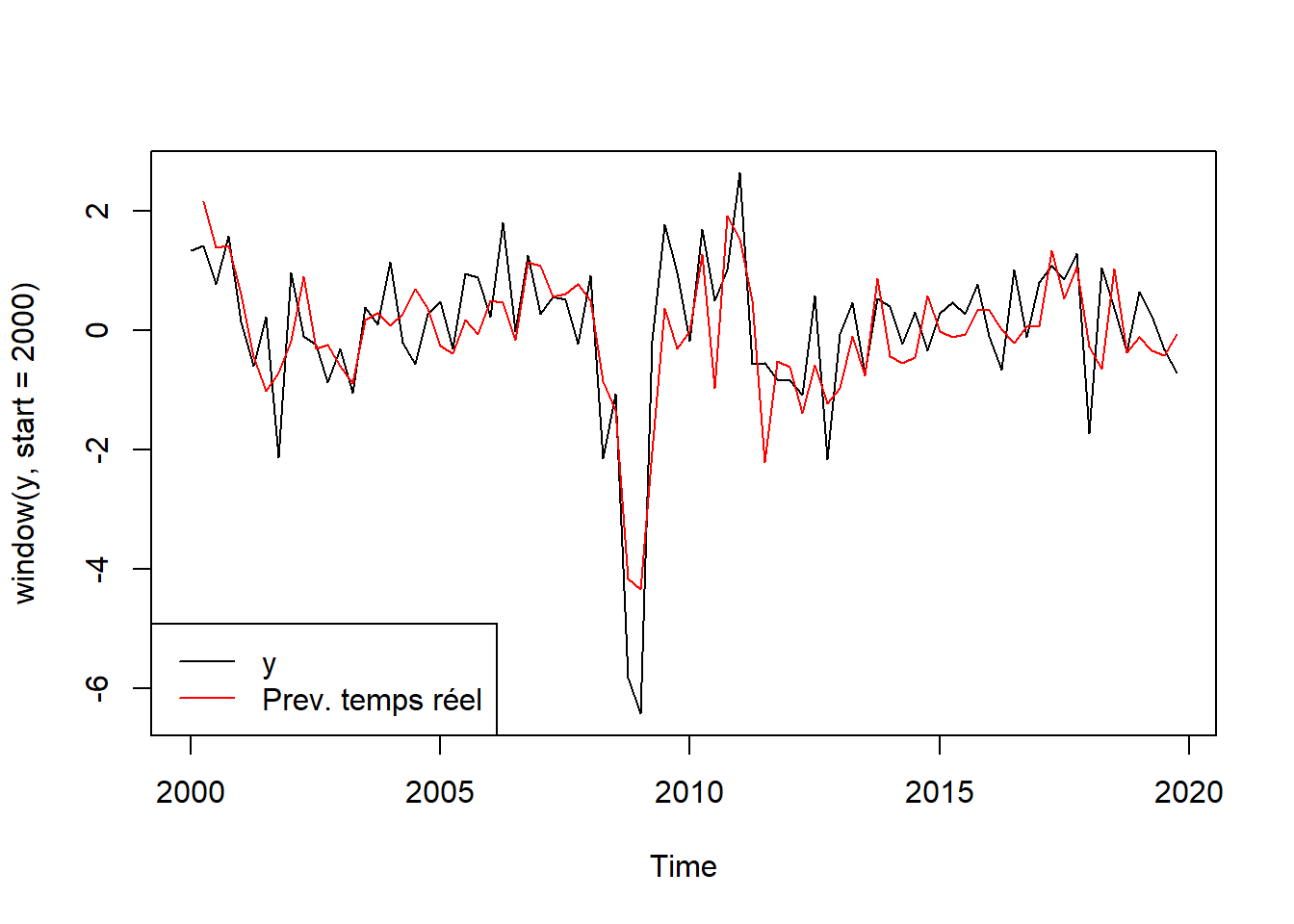

1 Régression par morceaux

Pour utiliser la régression par morceaux, la première étape est d’analyser les potentielles dates de rupture. Pour cela nous utiliserons la fonction tvCoef::piece_reg() (qui s’appuie sur le package strucchange, voir ?strucchange::breakpoints() pour plus d’informations).

Exercice

Utiliser la fonction tvCoef::piece_reg() sur le modèle précédent et regarder les résultats : y a-t-il des dates de ruptures ? Peuvent-elles être interprétées ?

En utilisant notamment oos_prev(), comparer la qualité prédictive des modèles.

Solution

reg_morceaux <- piece_reg(model_c5)
# Ici une date de rupture
# Si pas de rupture détectée, le modèle renvoyé est le modèle initial
reg_morceaux

$model

Time series regression with "ts" data:
Start = 1993(2), End = 2019(4)

Call:
dynlm::dynlm(formula = as.formula(formula), data = data2)

Coefficients:
               `(Intercept)_2008.75`              overhang_ipi1_c5_2008.75  
                             1.70092                               0.10847  
              insee_bc_c5_m3_2008.75              insee_oscd_c5_m2_2008.75  
                            -0.01335                               0.03653  
`diff(insee_tppre_c5_m3, 1)_2008.75`      `diff(bdf_tuc_c5_m2, 1)_2008.75`  
                             0.04306                               0.48388  
               `(Intercept)_2019.75`              overhang_ipi1_c5_2019.75  
                           -11.60377                               0.47441  
              insee_bc_c5_m3_2019.75              insee_oscd_c5_m2_2019.75  
                             0.10798                              -0.03376  
`diff(insee_tppre_c5_m3, 1)_2019.75`      `diff(bdf_tuc_c5_m2, 1)_2019.75`  
                             0.03414                               0.18874  


$start
[1] 1993    2

$end
[1] 2019    4

$frequency
[1] 4

$breakdates
[1] 2008.75

$tvlm
[1] FALSE

attr(,"class")
[1] "piecereg"

L’objet précédent est une liste qui contient différentes informations, notamment :

model : le modèle dynlm estimé ;
breakdates : la date de rupture : 2008T4.

Analysons maintenant les erreurs de prévision :

prev_oos_rm <- oos_prev(reg_morceaux)
res_rm_is <- residuals(reg_morceaux$model)
res_rm_oos <- prev_oos_rm$residuals
start(res_rm_oos) # Commence en 2000 T2

[1] 2000    2

rmse_rm <- c(IS = rmse(res_rm_is), OOS = rmse(res_rm_oos))
rbind(rmse_lm, rmse_rm)

               IS       OOS
rmse_lm 0.6990756 0.8494077
rmse_rm 0.5731039 1.3826525

Elle sont ici réduites dans l’échantillon mais augmentent en temps réel ! En regardant plus précisément, cela vient d’erreurs élevées autour de la date de rupture car l’estimation n’est pas suffisamment robuste !

plot(res_rm_oos, col = "red", main = "Résidus en temps-réel")
lines(res_lm_oos, col = "black")
legend("topleft", legend = c("LM","Reg. par morceaux"),
       col= c("black", "red"), lty = 1)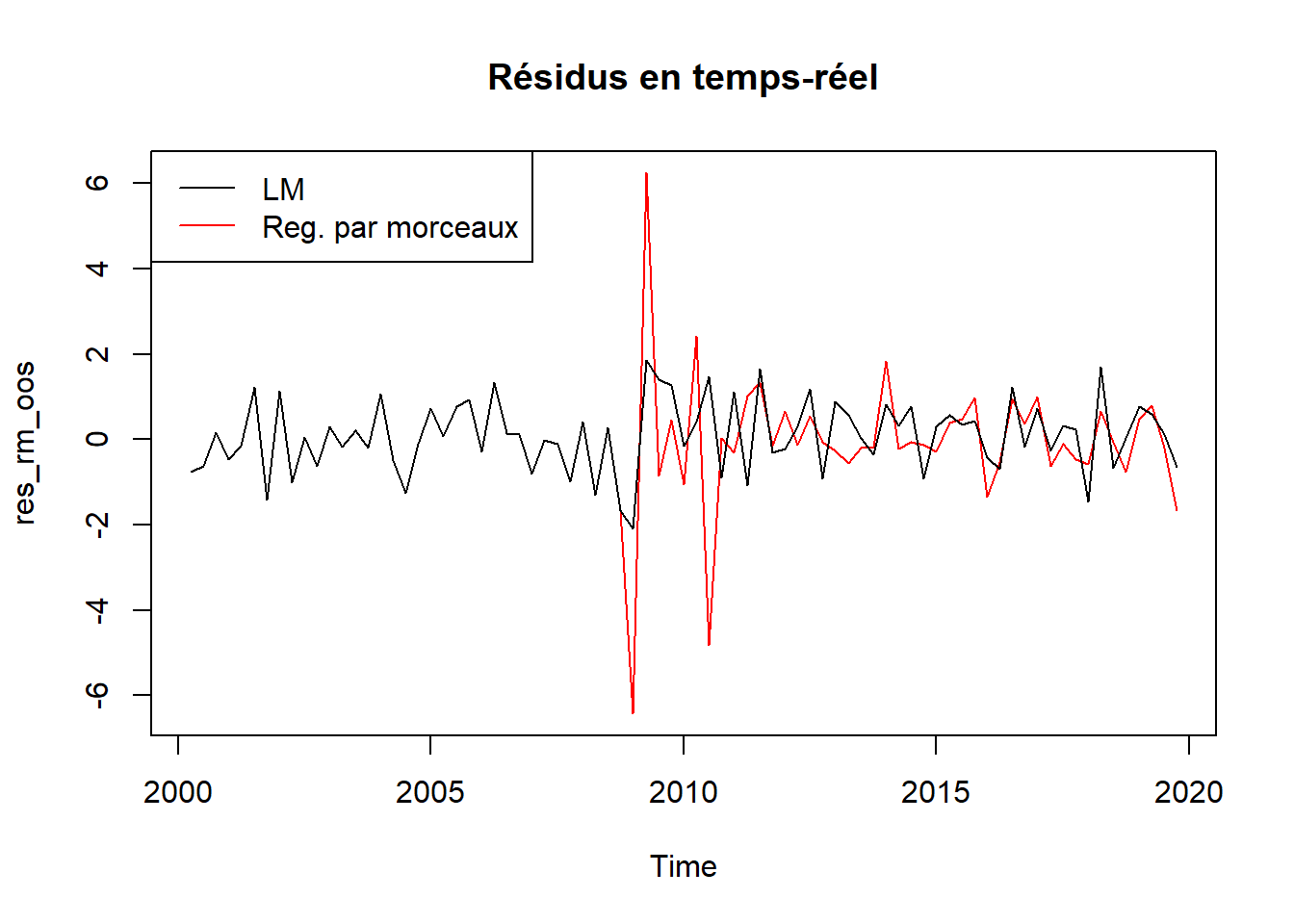

En analysant les prévisions à partir de 2010, les erreurs sont réduites par rapport à précédemment mais restent plus élevées que celles de la régression linéaire :

apply(window(ts.union(res_lm_oos, res_rm_oos), start = 2010), 2, rmse)

res_lm_oos res_rm_oos 
 0.7863127  1.1067406

Exercice

Le modèle précédent suppose une rupture sur toutes les variables : est-ce réaliste dans ce cas ? Appliquer la fonction tvCoef::hansen.test() sur votre modèle et interpréter les résultats.

Solution

hansen.test(model_c5)


Variable                  L        Stat     Conclusion 
______________________________________________________________ 
(Intercept)                  0.2561   0.47   FALSE   
overhang_ipi1_c5             0.8564   0.47    TRUE   
insee_bc_c5_m3               0.2708   0.47   FALSE   
insee_oscd_c5_m2             0.1508   0.47   FALSE   
diff(insee_tppre_c5_m3, 1)   0.2568   0.47   FALSE   
diff(bdf_tuc_c5_m2, 1)       0.1533   0.47   FALSE   
Variance                     0.4562   0.47   FALSE   
Joint Lc                     1.6516   2.11   FALSE   


Lecture: True means reject H0 at level 5%

Le test de Hansen conclut que seul l’acquis d’IPI évolue. Attention à l’interprétation du test sur la constante : si cette variable évolue il est possible que la constante aussi.

On peut également faire des tests de Fisher sur le modèle précédent pour tester si les coefficients sont égaux entre les sous-périodes. Cela peut être fait avec la fonction car::linearHypothesis() :

# on rejette H0 => non constance des coefficients
car::linearHypothesis(reg_morceaux$model, "`(Intercept)_2008.75` = `(Intercept)_2019.75`")

Linear hypothesis test

Hypothesis:
(Intercept)_2008.75` - Intercept)_2019.75` = 0

Model 1: restricted model
Model 2: y ~ 0 + (`(Intercept)_2008.75` + overhang_ipi1_c5_2008.75 + insee_bc_c5_m3_2008.75 + 
    insee_oscd_c5_m2_2008.75 + `diff(insee_tppre_c5_m3, 1)_2008.75` + 
    `diff(bdf_tuc_c5_m2, 1)_2008.75` + `(Intercept)_2019.75` + 
    overhang_ipi1_c5_2019.75 + insee_bc_c5_m3_2019.75 + insee_oscd_c5_m2_2019.75 + 
    `diff(insee_tppre_c5_m3, 1)_2019.75` + `diff(bdf_tuc_c5_m2, 1)_2019.75`)

  Res.Df    RSS Df Sum of Sq      F  Pr(>F)  
1     96 37.058                              
2     95 35.144  1    1.9145 5.1751 0.02516 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# on rejette H0 => non constance des coefficients
car::linearHypothesis(reg_morceaux$model, "overhang_ipi1_c5_2019.75 = overhang_ipi1_c5_2008.75")

Linear hypothesis test

Hypothesis:
- overhang_ipi1_c5_2008.75  + overhang_ipi1_c5_2019.75 = 0

Model 1: restricted model
Model 2: y ~ 0 + (`(Intercept)_2008.75` + overhang_ipi1_c5_2008.75 + insee_bc_c5_m3_2008.75 + 
    insee_oscd_c5_m2_2008.75 + `diff(insee_tppre_c5_m3, 1)_2008.75` + 
    `diff(bdf_tuc_c5_m2, 1)_2008.75` + `(Intercept)_2019.75` + 
    overhang_ipi1_c5_2019.75 + insee_bc_c5_m3_2019.75 + insee_oscd_c5_m2_2019.75 + 
    `diff(insee_tppre_c5_m3, 1)_2019.75` + `diff(bdf_tuc_c5_m2, 1)_2019.75`)

  Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
1     96 44.941                                  
2     95 35.144  1    9.7974 26.484 1.429e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# on ne rejette pas H0 => constance des coefficients
car::linearHypothesis(reg_morceaux$model, "`diff(insee_tppre_c5_m3, 1)_2019.75` = `diff(insee_tppre_c5_m3, 1)_2008.75`")

Linear hypothesis test

Hypothesis:
- diff(insee_tppre_c5_m3,_2008.75`  + diff(insee_tppre_c5_m3,_2019.75` = 0

Model 1: restricted model
Model 2: y ~ 0 + (`(Intercept)_2008.75` + overhang_ipi1_c5_2008.75 + insee_bc_c5_m3_2008.75 + 
    insee_oscd_c5_m2_2008.75 + `diff(insee_tppre_c5_m3, 1)_2008.75` + 
    `diff(bdf_tuc_c5_m2, 1)_2008.75` + `(Intercept)_2019.75` + 
    overhang_ipi1_c5_2019.75 + insee_bc_c5_m3_2019.75 + insee_oscd_c5_m2_2019.75 + 
    `diff(insee_tppre_c5_m3, 1)_2019.75` + `diff(bdf_tuc_c5_m2, 1)_2019.75`)

  Res.Df    RSS Df Sum of Sq      F Pr(>F)
1     96 35.201                           
2     95 35.144  1  0.056906 0.1538 0.6958

Exercice

En exploitant les résultats de l’exercice précédent, simplifier le modèle de régression par morceaux.

On pourra pour cela utiliser le paramètre fixed_var de piece_reg() pour fixer certaines variables (i.e. : ne pas découper les régresseurs).

Comparer les prévisions avec les modèles précédents.

Solution

Ici nous allons fixer toutes les variables sauf les deux premières (constante + acquis d’IPI – overhang)

reg_morceaux2 <- piece_reg(model_c5, fixed_var = c(3, 4, 5, 6))

# Rmq : la date de rupture est détectée sur le modèle complet et non
#  sur le sous-modèle avec des variables fixes
reg_morceaux2

$model

Time series regression with "ts" data:
Start = 1993(2), End = 2019(4)

Call:
dynlm::dynlm(formula = as.formula(formula), data = data2)

Coefficients:
              insee_bc_c5_m3              insee_oscd_c5_m2  
                    0.042179                      0.005864  
`diff(insee_tppre_c5_m3, 1)`      `diff(bdf_tuc_c5_m2, 1)`  
                    0.042554                      0.331692  
       `(Intercept)_2008.75`      overhang_ipi1_c5_2008.75  
                   -4.386765                      0.106947  
       `(Intercept)_2019.75`      overhang_ipi1_c5_2019.75  
                   -4.152134                      0.443726  


$start
[1] 1993    2

$end
[1] 2019    4

$frequency
[1] 4

$breakdates
[1] 2008.75

$tvlm
[1] FALSE

attr(,"class")
[1] "piecereg"

prev_oos_rm2 <- oos_prev(reg_morceaux2)
res_rm2_is <- residuals(reg_morceaux2$model)
res_rm2_oos <- prev_oos_rm2$residuals
rmse_rm2 <- c(IS = rmse(res_rm2_is), OOS = rmse(res_rm2_oos))
rbind(rmse_lm, rmse_rm, rmse_rm2)

                IS       OOS
rmse_lm  0.6990756 0.8494077
rmse_rm  0.5731039 1.3826525
rmse_rm2 0.6003532 0.8747103

# Après 2010
apply(window(ts.union(res_lm_oos, res_rm_oos, res_rm2_oos), start = 2010), 2, rmse)

 res_lm_oos  res_rm_oos res_rm2_oos 
  0.7863127   1.1067406   0.7050171

Cela permet d’améliorer la qualité de la prévision en temps-réel mais pas celle dans l’échantillon.

2 Régression locale

Pour rappel, la régression locale revient, pour chaque date $t$ à estimer $\beta_t$

\[ \DeclareMathOperator{\argmin}{argmin} \hat \beta = \underset{\theta_0}{\argmin}\sum_{j=1}^T\left(y_{j}-x_j\theta_0\right)^2K_b\left(\frac{j-t}{T}\right) \]

Dans le package ici utilisé (tvReg), le noyau utilisé par défaut est le noyau tricube :

\[ K(x)=\frac{35}{32}\left( 1- \left\lvert x \right\lvert^2 \right)^3 \mathbb 1_{|x| \leq 1} \text{ et } K_b(x)=\frac 1 b K(x/b) \]

Pour estimer le modèle, nous utilisons la fonction tvReg::tvLM dont le premier paramètre est une formule. Mais contrairement à dynlm, tvLM ne gère pas directement les variables en différence :

library(tvReg)
tvReg::tvLM(formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + insee_oscd_c5_m2
  + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 1),
  data = data)

Error in model.frame.default(formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + : les longueurs des variables diffèrent (trouvé pour 'diff(insee_tppre_c5_m3, 1)')

Pour éviter les problèmes liées au variables en différence, nous récupérons les données transformées de dynlm en utilisant la fonction tvCoef::get_data(model_c5), ce qui permet également de simplifier la formule en prod_c5 ~ .(puisque la base de données alors utilisée ne contient que les exogènes utiles).

Exercice

Estimer le modèle en utilisant les indications précédentes.

Quelle fenêtre est utilisée (paramètre $b$) ? Est-ce que les résultats sont différents de ceux de la régression linéaire ? Tracer les coefficients obtenus à chaque date (fonction coef() pour les extraire, il faudrait reconvertir le résultat en objet ts())

Comparer les erreurs de prévision dans l’échantillon avec ceux des modèles précédents.

Solution

La fenêtre retenue est de 0,31 : les résultats seront donc différents de ceux de la régression linéaire.

tvlm <- tvReg::tvLM(formula = prod_c5 ~ .,
                 data = get_data(model_c5))

Calculating regression bandwidth... bw =  0.4698719

coefs_tvlm <- ts(coef(tvlm), end = end(data), frequency = frequency(data))
plot(coefs_tvlm)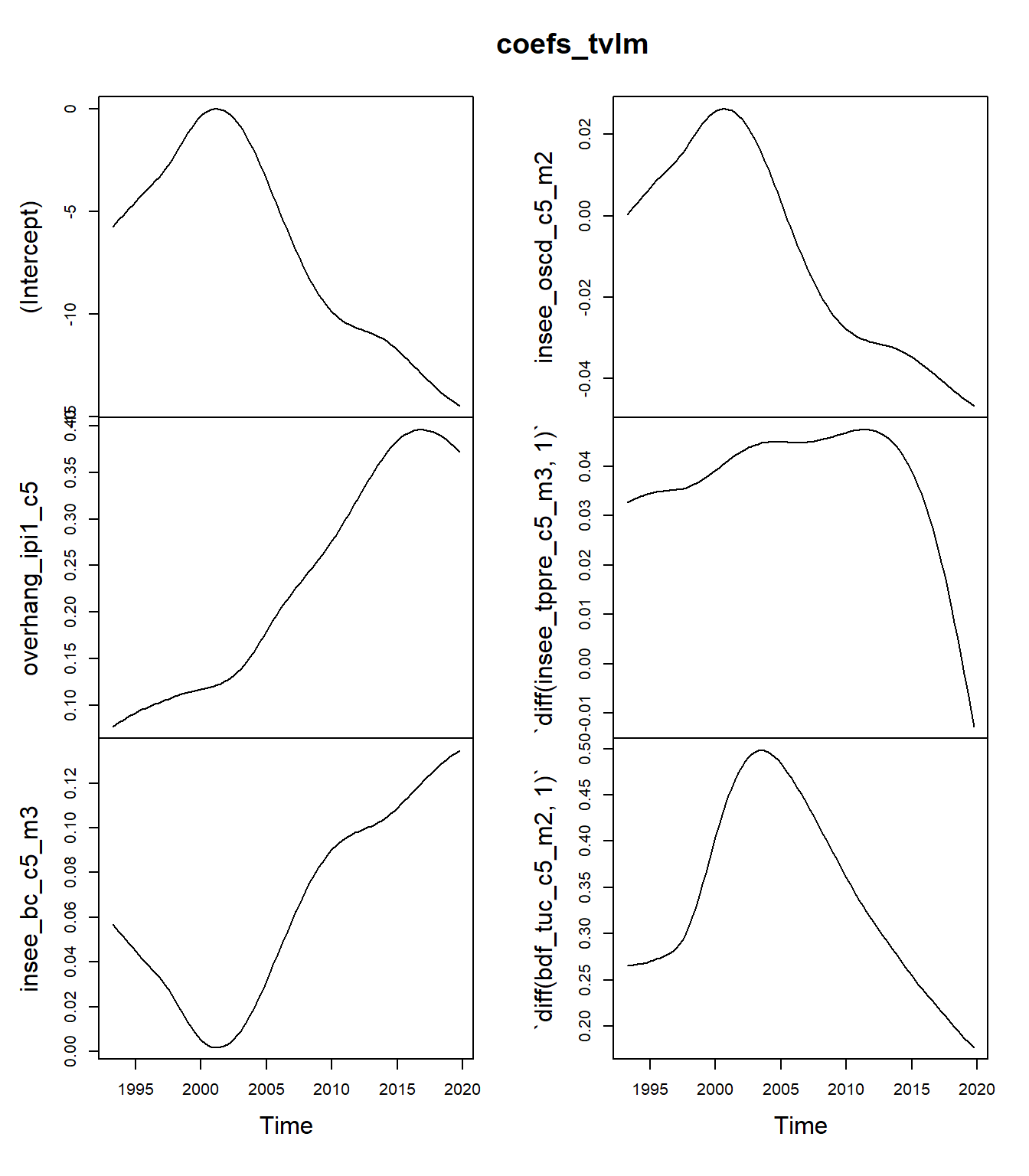

Ici toutes les coefficients sont variables alors que certains pourraient être fixes comme vu dans la partie précédente. Pour fixer certaines variables, on pourrait faire une régression en deux étapes.

res_tvlm_is <- residuals(tvlm)
rmse_tvlm <- c(IS = rmse(res_tvlm_is), OOS = NA)
rbind(rmse_lm, rmse_rm, rmse_rm2, rmse_tvlm)

                 IS       OOS
rmse_lm   0.6990756 0.8494077
rmse_rm   0.5731039 1.3826525
rmse_rm2  0.6003532 0.8747103
rmse_tvlm 0.5971192        NA

Le RMSE dans l’échantillon est réduit.

Exercice

L’objectif de cet exercice est de calculer les prévisions hors échantillon.

Appliquer la fonction tvCoef::oos_prev() au modèle précédent avec les paramètres end = end(data), frequency = frequency(data) (utiles pour garder la structure temporelle des données) : quels sont les paramètres réestimés ?

Appliquer maintenant la même fonction avec le paramètre fixed_bw = TRUE. À quoi cela correspond ? Comparer les erreurs de prévisions obtenus.

Solution

Dans les modèles de régression locales, il y a deux sources de révisions en temps-réel :

Actualisation des coefficients du fait de l’ajout de nouveaux points (noyau asymétrique utilisé pour les premières estimations)
Actualisation de la fenêtre.

Actualisation de la fenêtre et des coefficients

Par défaut, avec oos_prev() tous les paramètres sont réestimés. C’est en particulier le cas de la fenêtre qui est réestimée à chaque date, à chaque observation :

prev_oos_tvlm_all <- oos_prev(tvlm, end = end(data), frequency = frequency(data))

Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  20 
Calculating regression bandwidth... bw =  1.419831 
Calculating regression bandwidth... bw =  2.82952 
Calculating regression bandwidth... bw =  1.223547 
Calculating regression bandwidth... bw =  1.170575 
Calculating regression bandwidth... bw =  1.15924 
Calculating regression bandwidth... bw =  1.149263 
Calculating regression bandwidth... bw =  1.042411 
Calculating regression bandwidth... bw =  0.9797272 
Calculating regression bandwidth... bw =  0.4014617 
Calculating regression bandwidth... bw =  0.8781985 
Calculating regression bandwidth... bw =  0.4896312 
Calculating regression bandwidth... bw =  0.491814 
Calculating regression bandwidth... bw =  0.504626 
Calculating regression bandwidth... bw =  0.4866928 
Calculating regression bandwidth... bw =  0.3382399 
Calculating regression bandwidth... bw =  0.4753745 
Calculating regression bandwidth... bw =  0.4747202 
Calculating regression bandwidth... bw =  0.478007 
Calculating regression bandwidth... bw =  0.4662297 
Calculating regression bandwidth... bw =  0.4636153 
Calculating regression bandwidth... bw =  0.7847365 
Calculating regression bandwidth... bw =  0.7712849 
Calculating regression bandwidth... bw =  0.4601159 
Calculating regression bandwidth... bw =  0.4618806 
Calculating regression bandwidth... bw =  0.4630616 
Calculating regression bandwidth... bw =  0.4480051 
Calculating regression bandwidth... bw =  0.4333001 
Calculating regression bandwidth... bw =  0.4067395 
Calculating regression bandwidth... bw =  0.7120287 
Calculating regression bandwidth... bw =  0.7082321 
Calculating regression bandwidth... bw =  0.3906645 
Calculating regression bandwidth... bw =  0.3970553 
Calculating regression bandwidth... bw =  0.3421958 
Calculating regression bandwidth... bw =  0.3365896 
Calculating regression bandwidth... bw =  0.329112 
Calculating regression bandwidth... bw =  0.3323843 
Calculating regression bandwidth... bw =  0.649492 
Calculating regression bandwidth... bw =  0.4963082 
Calculating regression bandwidth... bw =  0.552225 
Calculating regression bandwidth... bw =  0.6002736 
Calculating regression bandwidth... bw =  0.5783915 
Calculating regression bandwidth... bw =  0.4433933 
Calculating regression bandwidth... bw =  0.4365778 
Calculating regression bandwidth... bw =  0.4698719

all_bw <- ts(sapply(prev_oos_tvlm_all$model, `[[`, "bw"),
             end = end(prev_oos_tvlm_all$prevision),
             frequency = frequency(data))
plot(all_bw)

res_tvlm_all_oos <- prev_oos_tvlm_all$residuals
rmse_tvlm["OOS"] <- rmse(res_tvlm_all_oos)
rbind(rmse_lm, rmse_rm, rmse_rm2, rmse_tvlm)

                 IS       OOS
rmse_lm   0.6990756 0.8494077
rmse_rm   0.5731039 1.3826525
rmse_rm2  0.6003532 0.8747103
rmse_tvlm 0.5971192 0.8595945

# Après 2010
apply(window(ts.union(res_lm_oos, res_rm_oos, res_rm2_oos, res_tvlm_all_oos), start = 2010), 2, rmse)

      res_lm_oos       res_rm_oos      res_rm2_oos res_tvlm_all_oos 
       0.7863127        1.1067406        0.7050171        0.8075138

Actualisation des coefficients uniquement

Fixons maintenant la fenêtre à la dernière valeur estimée :

prev_oos_tvlm_lastbw <- oos_prev(tvlm, end = end(data), frequency = frequency(data),fixed_bw = TRUE)
res_tvlm_lastbw_oos <- prev_oos_tvlm_lastbw$residuals
rmse_tvlm["OOS"] <- rmse(res_tvlm_lastbw_oos)
rbind(rmse_lm, rmse_rm, rmse_rm2, rmse_tvlm)

                 IS       OOS
rmse_lm   0.6990756 0.8494077
rmse_rm   0.5731039 1.3826525
rmse_rm2  0.6003532 0.8747103
rmse_tvlm 0.5971192 0.9799976

# Après 2010
apply(window(ts.union(res_lm_oos, res_rm_oos, res_rm2_oos, res_tvlm_all_oos, res_tvlm_lastbw_oos), start = 2010), 2, rmse)

         res_lm_oos          res_rm_oos         res_rm2_oos    res_tvlm_all_oos 
          0.7863127           1.1067406           0.7050171           0.8075138 
res_tvlm_lastbw_oos 
          0.7231632

Le RMSE en temps-réel est réduit par rapport à précédemment mais il reste plus élevé qu’avec la régression linéaire.

Remarque

Pour fixer certaines variables, on pourrait faire une régression en deux étapes. La fonction rmse_prev() permet de calculer les prévisions dans l’échantillon et hors échantillon sur le modèle de régression linéaire, la régression par morceaux, la régression locale en fixant ou non certains coefficients.

comp_prev <- rmse_prev(model_c5, fixed_var = c(3, 4, 5, 6), fixed_bw = TRUE)

Calculating regression bandwidth... bw =  0.4698719 
Calculating regression bandwidth... bw =  0.3501963

comp_prev

                       RMSE_in_sample RMSE_out_of_sample
lm                          0.6990756          0.8494077
piece_lm                    0.5731039          1.3826525
piece_lm fixed coeff        0.6003532          0.8747103
TvLM                        0.5971192          0.9799976
piece_tvlm                  0.5354897          1.4605933
piece_tvlm fixed coeff      0.5470547          1.0154322
TvLM fixed coeff            0.6254196          0.8574867

Sept modèles différents sont estimés, dans l’ordre :

Modèle de régression linéaire.
Régression linéaire par morceaux où toutes les variables divisées en fonction de la date de rupture.
Régression linéaire par morceaux où toutes les variables, sauf celles spécifiées par fixed_var, sont divisées en fonction de la date de rupture.
Régression locale.
Régression locale avec toutes les variables divisées en fonction de la date de rupture.
Régression locale où toutes les variables, sauf celles spécifiées par fixed_var, sont divisées en fonction de la date de rupture.
Régression locale où les variables celles spécifiées par fixed_var sont estimées par une régression linéaire (coefficients fixes sur l’ensemble de la période).

On peut ensuite récupérer tous les résidus en temps réel :

comp_prev_tr <- do.call(cbind, lapply(comp_prev$prevision, `[[`, "residuals"))
apply(window(comp_prev_tr, start = 2010), 2, rmse)

             prev_lm        prev_piece_lm   prev_piece_lm_fixe 
           0.7863127            1.1067406            0.7050171 
           prev_tvlm      prev_piece_tvlm prev_piece_tvlm_fixe 
           0.7231632            1.0894378            0.7072981 
      prev_tvlm_fixe 
           0.7246941

3 Modèles espace-état

Dans cette dernière partie nous estimons un modèle espace-état avec coefficients qui varient dans le temps.

Pour rappel, puisque nous avons 6 variables exogènes, le modèle s’écrit :

\[ \begin{cases} y_t=X_t\alpha_t+\varepsilon_t,\quad&\varepsilon_t\sim\mathcal N(0,\sigma^2)\\ \alpha_{t+1}=\alpha_t+\eta_t,\quad&\eta_t\sim\mathcal N(0,\sigma^2 Q) \end{cases},\text{ avec }\eta_t\text{ et }\varepsilon_t\text{ indépendants et } Q = \begin{pmatrix}q_1 & &0 \\ & \ddots \\ 0 & & q_6 \end{pmatrix} \]

La matrice $Q$ peut-être imposée par l’utilisateur (par exemple variance nulle si l’on veut fixer tous les coefficients) ou estimée.

Il y a également deux opérations classiques :

smoothing : estimation de $\hat\alpha_t=E[\alpha_t|y]$ et $V_t=V[\alpha_t-\hat\alpha_t]=V[\alpha_t|y]$ : coefficients et variances estimés en utilisant l’ensemble des données disponibles ;
filtering : estimation de $a_{t+1}=E[\alpha_{t+1}|Y_t]$ et $P_{t+1}=V[\alpha_{t+1}|Y_t]$ : coefficients et variances estimés de manière dynamique en utilisant l’information disponible jusqu’à la date précédente (estimation en temps-réel).

Pour estimer ces modèles nous utiliserons la fonction tvCoef::ssm_lm() dont le premier paramètre est un modèle de régression linéaire (le modèle model_c5).

Exercice

Par défaut, tvCoef::ssm_lm() estime le modèle en forçant $q_1=q_2=\dots=q_6=0$. Quel modèle retrouve-t-on ? Regarder les résultats de cette fonction et interpréter les quantités de "smoothed_states", "filtering_states","smoothed_stdev" (sauf dernière colonne).

Solution

Le modèle estimé est le modèle de régression linéaire !

La composante smoothed_states contient les coefficients du modèle de régression linéaire estimé en utilisant toutes les données. La dernière colonne ("noise") contient les résidus. La composante smoothed_stdev contient les écart-types associés aux différents coefficients, la dernière colonne s’interprète de manière plus complexe et ne sera pas détaillée ici.

mod_ssm <- ssm_lm(model_c5)
summary(model_c5)


Time series regression with "ts" data:
Start = 1993(2), End = 2019(4)

Call:
dynlm(formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + 
    insee_oscd_c5_m2 + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 
    1), data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.3241 -0.4566  0.0140  0.4495  1.6115 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept)                -6.383023   3.213333  -1.986  0.04970 *  
overhang_ipi1_c5            0.102405   0.022681   4.515 1.72e-05 ***
insee_bc_c5_m3              0.061437   0.029218   2.103  0.03797 *  
insee_oscd_c5_m2           -0.005596   0.015019  -0.373  0.71021    
diff(insee_tppre_c5_m3, 1)  0.039043   0.012029   3.246  0.00159 ** 
diff(bdf_tuc_c5_m2, 1)      0.397070   0.077580   5.118 1.48e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.7195 on 101 degrees of freedom
Multiple R-squared:  0.7155,    Adjusted R-squared:  0.7014 
F-statistic: 50.79 on 5 and 101 DF,  p-value: < 2.2e-16

tail(mod_ssm$smoothed_states, 3)

       (Intercept) overhang_ipi1_c5 insee_bc_c5_m3 insee_oscd_c5_m2
[105,]   -6.383023        0.1024052     0.06143715     -0.005596399
[106,]   -6.383023        0.1024052     0.06143715     -0.005596399
[107,]   -6.383023        0.1024052     0.06143715     -0.005596399
       diff(insee_tppre_c5_m3, 1) diff(bdf_tuc_c5_m2, 1)      noise
[105,]                 0.03904254              0.3970705  0.5785851
[106,]                 0.03904254              0.3970705  0.1141372
[107,]                 0.03904254              0.3970705 -0.6226152

tail(mod_ssm$smoothed_stdev, 3)

       (Intercept) overhang_ipi1_c5 insee_bc_c5_m3 insee_oscd_c5_m2
[105,]    3.213333       0.02268142     0.02921753       0.01501868
[106,]    3.213333       0.02268142     0.02921753       0.01501868
[107,]    3.213333       0.02268142     0.02921753       0.01501868
       diff(insee_tppre_c5_m3, 1) diff(bdf_tuc_c5_m2, 1)     noise
[105,]                 0.01202881             0.07757954 0.1554965
[106,]                 0.01202881             0.07757954 0.1367629
[107,]                 0.01202881             0.07757954 0.1460395

La composante filtering_states donne les estimations des coefficients en temps réel : la valeur à la date $t$ correspond aux estimations des coefficients en utilisant les données jusqu’en $t-1$. Ainsi, en estimant le modèle jusqu’en 2010T1, les coefficients obtenus sont ceux de la composante filtering_states de 2010T2 :

summary(dynlm(
  formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + insee_oscd_c5_m2
  + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 1),
  data = window(data, end = 2010)
))


Time series regression with "ts" data:
Start = 1993(2), End = 2010(1)

Call:
dynlm(formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + 
    insee_oscd_c5_m2 + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 
    1), data = window(data, end = 2010))

Residuals:
     Min       1Q   Median       3Q      Max 
-1.93741 -0.36837 -0.02174  0.41270  1.50865 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept)                 0.687568   4.010977   0.171 0.864451    
overhang_ipi1_c5            0.096558   0.029839   3.236 0.001947 ** 
insee_bc_c5_m3             -0.003804   0.036838  -0.103 0.918081    
insee_oscd_c5_m2            0.027262   0.018837   1.447 0.152869    
diff(insee_tppre_c5_m3, 1)  0.047953   0.013331   3.597 0.000639 ***
diff(bdf_tuc_c5_m2, 1)      0.595962   0.104419   5.707 3.46e-07 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6887 on 62 degrees of freedom
Multiple R-squared:  0.8058,    Adjusted R-squared:  0.7902 
F-statistic: 51.46 on 5 and 62 DF,  p-value: < 2.2e-16

window(mod_ssm$filtering_states, start = 2010, end = c(2010,2))

        (Intercept) overhang_ipi1_c5 insee_bc_c5_m3 insee_oscd_c5_m2
2010 Q1   0.4262027       0.09515354   -0.001352874       0.02587391
2010 Q2   0.6875678       0.09655775   -0.003804293       0.02726163
        diff(insee_tppre_c5_m3, 1) diff(bdf_tuc_c5_m2, 1) noise
2010 Q1                 0.04759521              0.5960833     0
2010 Q2                 0.04795263              0.5959618     0

Exercice

Estimer maintenant le modèle en utilisant les paramètres suivants :

model_ssm <- ssm_lm(model_c5,
       var_intercept = 0.01, fixed_var_intercept = FALSE,
       var_variables = 0.01, fixed_var_variables = FALSE)

Les paramètres fixed_var_intercept = FALSE et fixed_var_variables = FALSE permettent d’indiquer que les variances $q_1,\dots, q_6$ seront estimées. Les paramètres var_intercept et var_variables n’auront généralement aucun impact sur les résultats (puisque dans notre cas les variances sont estimées), ils interviennent toutefois dans le processus algorithmique : les modifier permet dans certains cas d’éviter des erreurs d’optimisation.

Regarder les coefficients model_ssm$smoothed_states : quelles sont les variables qui varient dans le temps ? À partir de model_ssm$fitted, comparer la qualité prédictive de ce modèle avec les précédents.

Solution

Les variables fixes sont la constante et les carnets de commandes globaux :

plot(model_ssm$smoothed_states[,-ncol(model_ssm$smoothed_states)])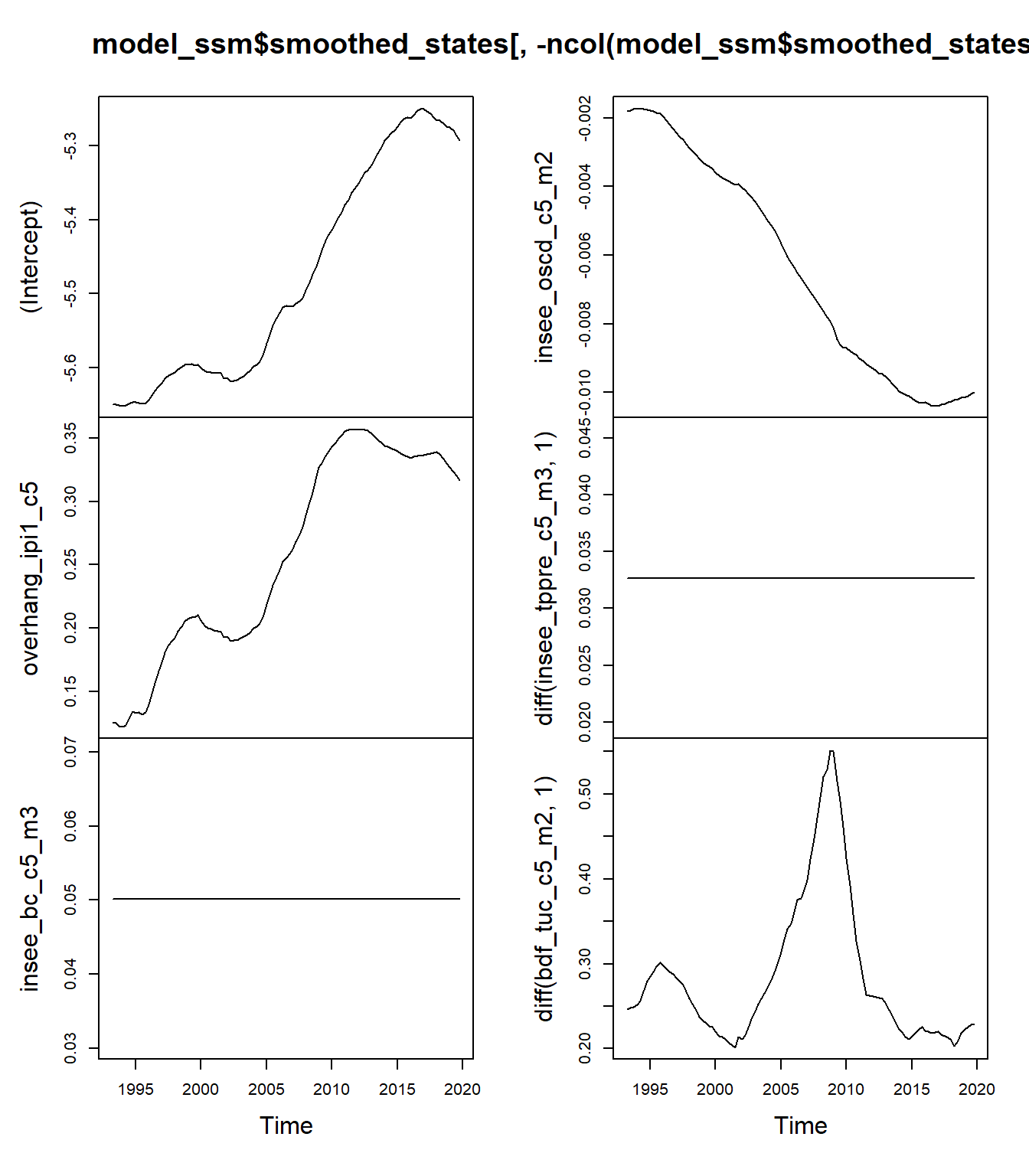

On peut également vérifier en regardant les variances $\sigma^2q_i$ :

model_ssm$parameters$parameters * model_ssm$parameters$scaling

               (Intercept).var           overhang_ipi1_c5.var 
                  1.870276e-03                   3.863439e-04 
            insee_bc_c5_m3.var           insee_oscd_c5_m2.var 
                  0.000000e+00                   1.097830e-06 
diff(insee_tppre_c5_m3, 1).var     diff(bdf_tuc_c5_m2, 1).var 
                  0.000000e+00                   3.462322e-03 
                     noise.var 
                  3.548244e-01

res_ssm_is <- y - model_ssm$fitted[,"smoothed"]
res_ssm_oos <- y - model_ssm$fitted[,"filtering"]
rmse_ssm <- c(IS = rmse(res_ssm_is), OOS = rmse(res_ssm_oos))
rbind(rmse_lm, rmse_rm, rmse_rm2, rmse_tvlm, rmse_ssm)

                 IS       OOS
rmse_lm   0.6990756 0.8494077
rmse_rm   0.5731039 1.3826525
rmse_rm2  0.6003532 0.8747103
rmse_tvlm 0.5971192 0.9799976
rmse_ssm  0.5422771 0.7441522

# Après 2010
apply(window(ts.union(res_lm_oos, res_rm_oos, res_rm2_oos, res_tvlm_lastbw_oos, res_ssm_oos), start = 2010), 2, rmse)

         res_lm_oos          res_rm_oos         res_rm2_oos res_tvlm_lastbw_oos 
          0.7863127           1.1067406           0.7050171           0.7231632 
        res_ssm_oos 
          0.6863295

En réalité, la composante filtering ne correspond pas exactement à de l’estimation en temps-réel car certains paramètres ne sont pas estimés de manière dynamique. Pour avoir une vraie estimation en temps-réel, il faudrait réestimer le modèle à chaque date : on peut pour cela utiliser la fonction ssm_lm_oos(). Pour que cette fonction marche, il faut parfois jouer sur les paramètres var_intercept et var_variables.

model_ssm_oos <- ssm_lm_oos(model_c5,
       var_intercept = 0.001, fixed_var_intercept = FALSE,
       var_variables = 0.001, fixed_var_variables = FALSE)
res_ssm_oos <- y - model_ssm_oos$prevision

rmse_ssm <- c(IS = rmse(res_ssm_is), OOS = rmse(res_ssm_oos))
rbind(rmse_lm, rmse_rm, rmse_rm2, rmse_tvlm, rmse_ssm)

                 IS       OOS
rmse_lm   0.6990756 0.8494077
rmse_rm   0.5731039 1.3826525
rmse_rm2  0.6003532 0.8747103
rmse_tvlm 0.5971192 0.9799976
rmse_ssm  0.5422771 0.7337112

apply(window(ts.union(res_lm_oos, res_rm_oos, res_rm2_oos, res_tvlm_lastbw_oos, res_ssm_oos), start = 2010), 2, rmse)

         res_lm_oos          res_rm_oos         res_rm2_oos res_tvlm_lastbw_oos 
          0.7863127           1.1067406           0.7050171           0.7231632 
        res_ssm_oos 
          0.6571734

On peut enfin faire un graphique avec toutes les prévisions, en utilisant par exemple le package dygraphs :

library(dygraphs)
prevs <- ts.intersect(y, y - res_lm_oos, y - res_rm2_oos, y - res_tvlm_lastbw_oos, y - res_ssm_oos)
colnames(prevs) <- c("y", "lm", "Reg par morceaux", "Reg locale", "SSM")
dygraph(prevs) %>% 
  dyRangeSelector(dateWindow = c("2010-01-01", "2019-12-01")) %>%
  dyOptions(colors = c("black", "red", "green", "blue", "purple"))

Exercice facultatif

L’objectif de cet exercice est d’estimer un nouveau modèle jusqu’en 2022T4 pour faire une prévision jusqu’en 2023T1 :

Créer des indicatrices sur les 4 premiers trimestres de l’année 2020.
Estimer un nouveau modèle dynlm en ajoutant ces indicatrices.
Estimer un nouveau modèle espace-état.
Utiliser les variables exogènes du modèle jusqu’en 2023T1 (on peut pour cela appliquer la fonction tvCoef::full_exogeneous_matrix() sur le modèle dynlm) et la dernière ligne de la composante "smoothed_states" pour effectuer des prévisions sur 2023T1.

Indice (création des indicatrices)

On pourra utiliser le programme suivant pour créer les indicatrices :

ind <- cbind(time(manufacturing) == 2020, time(manufacturing) == 2020.25, time(manufacturing) == 2020.5,
time(manufacturing) == 2020.75)
ind <- ts(apply(ind,2, as.numeric), start = start(manufacturing), frequency = 4)
colnames(ind) <- sprintf("ind2020Q%i", 1:4)
data <- ts.union(manufacturing, ind)
colnames(data) <- c(colnames(manufacturing), colnames(ind))

Solution

Estimation du modèle de régression linéaire :

ind <- cbind(time(manufacturing) == 2020, time(manufacturing) == 2020.25, time(manufacturing) == 2020.5,
time(manufacturing) == 2020.75)
ind <- ts(apply(ind,2, as.numeric), start = start(manufacturing), frequency = 4)
colnames(ind) <- sprintf("ind2020Q%i", 1:4)
data <- ts.union(manufacturing, ind)
colnames(data) <- c(colnames(manufacturing), colnames(ind))

data <- ts.union(manufacturing, ind)
colnames(data) <- c(colnames(manufacturing), colnames(ind))
model_c5_complet <- dynlm(
  formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + insee_oscd_c5_m2
  + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 1) 
  + ind2020Q1 + ind2020Q2 + ind2020Q3 + ind2020Q4,
  data = data
)
summary(model_c5_complet)


Time series regression with "ts" data:
Start = 1990(2), End = 2022(4)

Call:
dynlm(formula = prod_c5 ~ overhang_ipi1_c5 + insee_bc_c5_m3 + 
    insee_oscd_c5_m2 + diff(insee_tppre_c5_m3, 1) + diff(bdf_tuc_c5_m2, 
    1) + ind2020Q1 + ind2020Q2 + ind2020Q3 + ind2020Q4, data = data)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.50121 -0.40188  0.00267  0.48994  1.57418 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept)                -6.924304   3.182453  -2.176   0.0315 *  
overhang_ipi1_c5            0.115792   0.020951   5.527 1.91e-07 ***
insee_bc_c5_m3              0.065321   0.028967   2.255   0.0259 *  
insee_oscd_c5_m2           -0.009964   0.014757  -0.675   0.5008    
diff(insee_tppre_c5_m3, 1)  0.026459   0.011405   2.320   0.0220 *  
diff(bdf_tuc_c5_m2, 1)      0.361476   0.077713   4.651 8.49e-06 ***
ind2020Q1                  -5.195550   0.788939  -6.585 1.23e-09 ***
ind2020Q2                  -7.650566   1.654785  -4.623 9.53e-06 ***
ind2020Q3                  16.223534   1.482828  10.941  < 2e-16 ***
ind2020Q4                   3.324056   0.810984   4.099 7.55e-05 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.7705 on 121 degrees of freedom
  (131 observations effacées parce que manquantes)
Multiple R-squared:  0.9393,    Adjusted R-squared:  0.9348 
F-statistic: 208.1 on 9 and 121 DF,  p-value: < 2.2e-16

prev_oos_lm_complet <- oos_prev(model_c5_complet)

Estimation du modèle espace-état :

model_ssm_complet <- ssm_lm(model_c5_complet,
       var_intercept = 0.01, fixed_var_intercept = FALSE,
       var_variables = 0.01, fixed_var_variables = FALSE)
# # Rmq : on pourrait également fixer à 0 les variances des coefficients associées aux indicatrices :
# model_ssm_complet <- ssm_lm(model_c5_complet,
#         var_intercept = 0.01, fixed_var_intercept = FALSE,
#         var_variables = c(rep(0.01,5), rep(0, 4)), 
#         fixed_var_variables = c(rep(FALSE,5), rep(TRUE, 4)))

model_ssm_complet_oos <- ssm_lm_oos(model_c5_complet, date = 18*4,
       var_intercept = 0.01, fixed_var_intercept = FALSE,
       var_variables = 0.01, fixed_var_variables = FALSE)

Enfin, pour calculer les prévisions

X_variables = full_exogeneous_matrix(model_c5_complet)
window(X_variables, start = 2022)

        (Intercept) overhang_ipi1_c5 insee_bc_c5_m3 insee_oscd_c5_m2
2022 Q1           1         7.629539          108.0              4.5
2022 Q2           1         2.870669          105.8             -2.2
2022 Q3           1         2.663170           97.9            -16.0
2022 Q4           1         1.979440           96.2            -24.6
2023 Q1           1         1.737138           98.7            -23.0
        diff(insee_tppre_c5_m3, 1) diff(bdf_tuc_c5_m2, 1) ind2020Q1 ind2020Q2
2022 Q1                      -20.1                  -0.23         0         0
2022 Q2                        0.1                   0.53         0         0
2022 Q3                       -9.7                   0.57         0         0
2022 Q4                       10.1                  -1.88         0         0
2023 Q1                       -1.9                  -0.49         0         0
        ind2020Q3 ind2020Q4
2022 Q1         0         0
2022 Q2         0         0
2022 Q3         0         0
2022 Q4         0         0
2023 Q1         0         0

prevs_lm <- rowSums(X_variables %*% diag(coef(model_c5_complet)))
prevs_lm <- prevs_lm[length(prevs_lm)]
prevs_ssm <- rowSums(X_variables %*% diag(model_ssm_complet$smoothed_states[nrow(model_ssm_complet$smoothed_states), - ncol(model_ssm_complet$smoothed_states)]))
prevs_ssm <- prevs_ssm[length(prevs_ssm)]
full_prevs <- ts.union(prev_oos_lm_complet$prevision,
                       model_ssm_complet_oos$prevision)
full_prevs <- ts(rbind(full_prevs,
                       c(prevs_lm, prevs_ssm)),
                 start = start(full_prevs),
                 frequency = frequency(full_prevs))
data_forecasts <- ts.union(manufacturing[,"prod_c5"], full_prevs)
data_forecasts <- window(data_forecasts, start = 2010)
colnames(data_forecasts) <- c("y", "lm", "SSM")
dygraph(data_forecasts) %>% 
  dyRangeSelector(dateWindow = c("2018-01-01", "2023-03-01"))

Notes de bas de page

L’avantage de dynlm par rapport à lm est qu’il permet de gérer directement la différenciation des variables sans avoir à créer de variable temporaire.↩︎